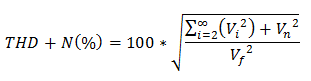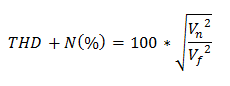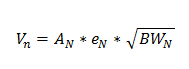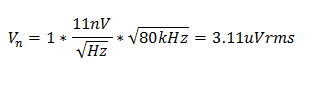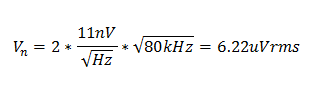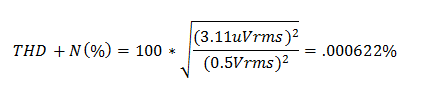噪声和失真是工程师在设计高精度模拟系统常见的两个令人挠头的问题。但是,当我们查看一个运算放大器数据表中的总谐波失真和噪声 (THD+N) 数值时,也许不能立即搞清楚哪一个才是你要应对的敌人:噪声还是失真?
“噪声”描述的是由放大器产生的随机电信号。“失真”是指由放大器引入的有害谐波。谐波是频率为输入信号频率整数倍的信号。总谐波失真和噪声技术规格通过比较失真谐波的电平 (Vi) 和RMS噪声电压 (Vn) 与输入信号的电平 (Vf) 来量化这些因素,使用的方程式如下:
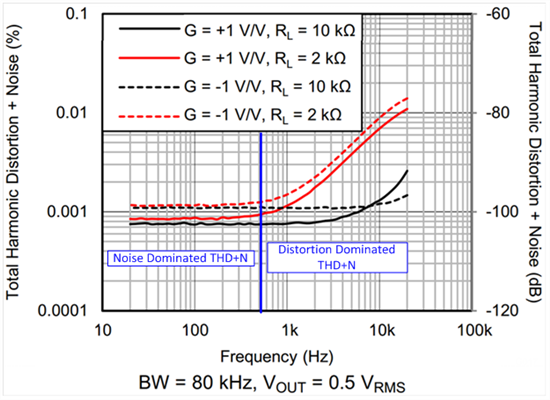
在OPA316的数据表中,这条曲线显示了针对多个配置和输出负载,在频率范围内测得的THD+N。不幸的是,我们无法立即知道噪声或失真谐波是否对THD+N有更大的影响。要深入探究这一点,我们可以计算噪声对测量结果产生的影响。
图1:多个配置之后THD+N与OPA316的频率之间的关系
首先,我们简化THD+N计算来去除失真项:
我们可以用如下方程式来近似计算一个基本运算放大器电路的RMS噪声电压:
AN 是“噪声增益”,eN是运算放大器宽带电压噪声频谱密度,而BWN是测量噪声时的带宽。噪声增益,或者说是放大器对其固有噪声的增加,始终在运算放大器的非反向输入上测得。当运算放大器被用作非反向放大器时,这种方法简单且直接;信号增益与噪声增益是一样的。然而,对于反向放大器,噪声增益将为信号增益的幅值加上1。例如,信号增益为-1的反向放大器具有+2的噪声增益。
OPA316有一个11nV/√Hz的宽带输入电压噪声频谱密度,并且测量带宽的额定值为80kHz。对于非反向放大器 (G = +1),RMS噪声电压大约为:
对于反向放大器(增益 = -1),RMS噪声电压为:
现在,可使用下图给出的输出幅值信息来计算这两个配置中噪声对THD+N测量值的影响:
非反向 (G = +1):
反向 (G = -1):
请注意,这些计算出来的值与低频下 (<500Hz) 测得的THD+N密切对应。在这里,测量值几乎完全由运算放大器的噪声决定。由于输入信号的频率不影响噪声电压,噪声优势频率上的THD+N测量值在是扁平的。
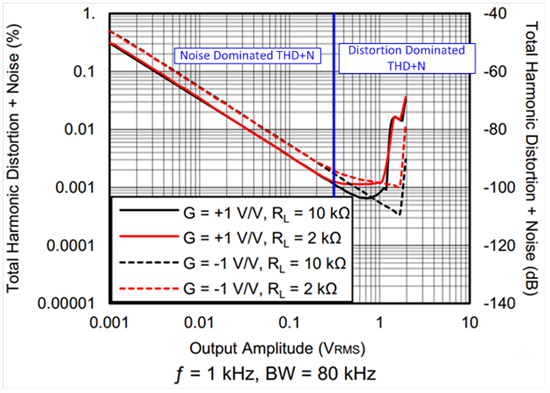
相似的,在低信号幅值上,THD+N测量值主要受噪声影响。图2显示1kHz时,在OPA316上测得的THD+N与输出幅值之间的关系。在300mV以下时,两个输出曲线具有一个恒定斜率。RMS噪声是恒定的,而与输入信号幅值无关,所以信号幅值的增加会改进THD+N的测量值。例如,在曲线的噪声主导区域,把输出幅值加倍将使THD+N的值减半。
图2:多个配置中,OPA316运行在1kHz时,THD+N与输出幅值之间的关系
另一方面,失真谐波的幅值会随着信号幅值的变化而变化。一旦曲线偏离恒定向下斜坡,我们就会知道失真谐波正在影响THD+N测量值。
针对低噪声的电路设计具有噪声不断增加带来的有害后果。具有低值反馈电阻器的非反向运算放大器可以提供特别低的噪声,但是额外的负载和共模电压会增加高频失真。了解噪声或失真是否会限制你的系统性能对于找到一个工程设计解决方案十分关键。掌握某些基本手算结果,并且能够看懂数据表THD+N图,你就可以迅速确定谁是罪魁祸首了。
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||