当前位置:首 页 --> 技术分享
利用FIR滤波器去除传输线效应
发布时间:2016/12/30 16:11:00 来源:
网络串行解串器(SERDES)的串行数据输出速度已经高达28Gbps,并且还在继续发展。在如此高数据速率的条件下,即使很短的PCB走线也会起到传输线的作用,进而通过衰减和散射降低信号完整性。在芯片的焊球上监视SERDES发送器输出信号很难做到。通常信号会引到SMA或SMP连接器后再用示波器进行监测。然而,信号特性会因为IC和连接器之间的传输线而发生改变。因此,真正的挑战是在SERDES引脚处监视信号性能,而这可以通过去除传输线效应来实现。本设计实例介绍了一种去除传输线的方法。
假设H(s)是走线的冲激响应,如果X(s)是输入信号,那么从数学角度看:
Y(s)=H(s)×X(s)
X(s)=Y(s)×H-1(s)
可以将H-1(s)实现为有限冲激响应(FIR)滤波器,并使用MATLAB确定滤波系数(参考文章最后的文档)。
走线的H(s)可以用网络分析仪进行测量,测量的对象是Sdd21.首先需要确定FIR滤波器(hf(t))的系数,其频率响应(Hf(s))接近上述测量的Sdd21的倒数,即Hf(s)=H-1(s)。计算滤波器系数的方法是先从特定系数开始计算频率响应,然后计算H(s)和Hf(s)之间的幅度误差。最后使用优化算法改变系数,直到使和方差最小。
参考FIR_filter_design.m,nc是FIR滤波器中的系数值,drate是单位为Gbps的输入串行数据的数据速率。选择合适的fs,使fs/drate为整数。这样将定义用1个比特表示的系数值。Ncbit给出了相邻系数间的时间差。假设N是频率响应Hf(s)中的点数,numfpts=N/2是奈奎斯特范围内的频点数。滤波器传递函数的奈奎斯特频率就是fs/2.然后定义finmin到finmax的频率范围,这样就可以计算这个范围内的幅度误差了。
对应奈奎斯特的滤波器频率点为:
Hz1=(k×fs)/(2×numfpts),k=0~numpts-1
插值运算是通过计算Hz1频率点处的Sdd21幅度完成的。将滤波系数初始化为某个值。使用freqz MATLAB函数计算滤波器的频率响应幅度,然后确定插值后获得的Sdd21幅度数据间的误差。使用MATLAB fminbnd函数可以最大程度地减小和方差,最小化算法有许多实现方式,本文提供的代码只是其中一种。
实验结果
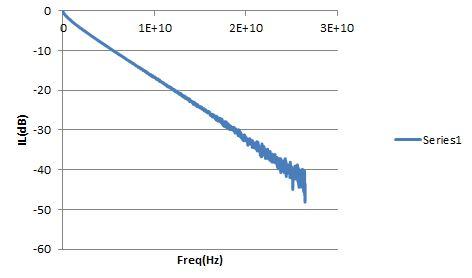
为了演示FIR滤波器的效果,使用一台Keysight 86100D采样示波器和一台Tektronix的BERTScope,生成了速率为10.3125Gbps的图案。BERTScope的输出连接到DS0,波形存储在示波器内存中,如图1所示(洋红色)。然后将BERTScope输出连接到PCB上的传输线;通道的SDD21(dB)的变化如图2所示。将通道的输出连接到DS0(黄线)。通道引起的衰减和散射显著劣化了波形。在示波器的数学功能选项中有一个线性均衡器模块,它的输入是滤波系数。在信号路径中插入该线性均衡器模块,然后输入滤波系数。该模块的输出用绿线表示。FIR滤波器消除了通道的ISI效应,而且恢复的波形相当完美。
假设H(s)是走线的冲激响应,如果X(s)是输入信号,那么从数学角度看:
Y(s)=H(s)×X(s)
X(s)=Y(s)×H-1(s)
可以将H-1(s)实现为有限冲激响应(FIR)滤波器,并使用MATLAB确定滤波系数(参考文章最后的文档)。
走线的H(s)可以用网络分析仪进行测量,测量的对象是Sdd21.首先需要确定FIR滤波器(hf(t))的系数,其频率响应(Hf(s))接近上述测量的Sdd21的倒数,即Hf(s)=H-1(s)。计算滤波器系数的方法是先从特定系数开始计算频率响应,然后计算H(s)和Hf(s)之间的幅度误差。最后使用优化算法改变系数,直到使和方差最小。
参考FIR_filter_design.m,nc是FIR滤波器中的系数值,drate是单位为Gbps的输入串行数据的数据速率。选择合适的fs,使fs/drate为整数。这样将定义用1个比特表示的系数值。Ncbit给出了相邻系数间的时间差。假设N是频率响应Hf(s)中的点数,numfpts=N/2是奈奎斯特范围内的频点数。滤波器传递函数的奈奎斯特频率就是fs/2.然后定义finmin到finmax的频率范围,这样就可以计算这个范围内的幅度误差了。
对应奈奎斯特的滤波器频率点为:
Hz1=(k×fs)/(2×numfpts),k=0~numpts-1
插值运算是通过计算Hz1频率点处的Sdd21幅度完成的。将滤波系数初始化为某个值。使用freqz MATLAB函数计算滤波器的频率响应幅度,然后确定插值后获得的Sdd21幅度数据间的误差。使用MATLAB fminbnd函数可以最大程度地减小和方差,最小化算法有许多实现方式,本文提供的代码只是其中一种。
实验结果
为了演示FIR滤波器的效果,使用一台Keysight 86100D采样示波器和一台Tektronix的BERTScope,生成了速率为10.3125Gbps的图案。BERTScope的输出连接到DS0,波形存储在示波器内存中,如图1所示(洋红色)。然后将BERTScope输出连接到PCB上的传输线;通道的SDD21(dB)的变化如图2所示。将通道的输出连接到DS0(黄线)。通道引起的衰减和散射显著劣化了波形。在示波器的数学功能选项中有一个线性均衡器模块,它的输入是滤波系数。在信号路径中插入该线性均衡器模块,然后输入滤波系数。该模块的输出用绿线表示。FIR滤波器消除了通道的ISI效应,而且恢复的波形相当完美。
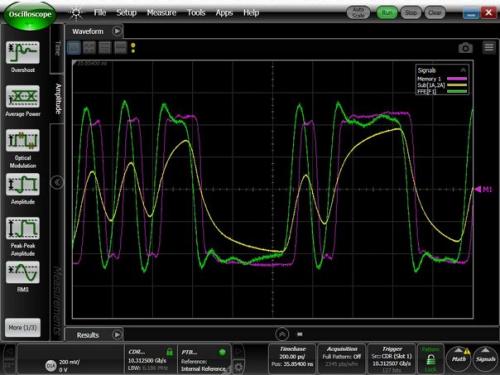
图1:BerScope PRBS7输出(洋红色);PCB走线输出端的信号(黄色);FIR滤波器输出(绿色)。
从MATLAB代码获得的FIR系数是:
0.766, -0.115, -0.097, -0.119, -0.090, -0.099,-0.083, -0.033, 0.028, 0.015, 0.042, 0.013, 0.024,-0.008, 0.002, -0.019, 0.000, -0.025, 0.005,-0.014, 0.011, -0.007, 0.021, -0.002, 0.014,-0.009, 0.009, -0.018, 0.003, -0.022.
本文小结
通过消除PCB走线引起的衰减,滤波器极大地提高了信号完整性。这个过程可以用示波器、离线式或硬件实现等方式进行。
BertScope输出和滤波器输出之间存在一些差异,引起这些差异的原因是:
●第一个用户界面(UI)中存在一些尖峰。这是滤波系数a2、a3和a4的值较大引起的。大多数高频放大是通过这些系数完成的,因此会引起尖峰。通过修改算法可以加以纠正。
●应该使用低通滤波(LPF)函数对H1(s)加以频带限制。这将形成频带受限的滤波器,并在整个传递函数上尽量减少误差。这样也有望减小第一个UI中的峰值。本文中的滤波器是通过定义fmin和fmax实现频带受限的,这种方法会引入一定的误差。
●在确定滤波器系数时没有包含相位信号,这也会引入一定的误差。
通过在设计算法中采取这些校正措施,可以改进滤波系数的计算。
|
||||||
|
||||||