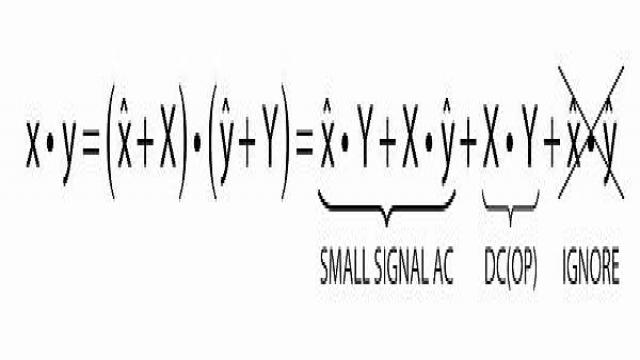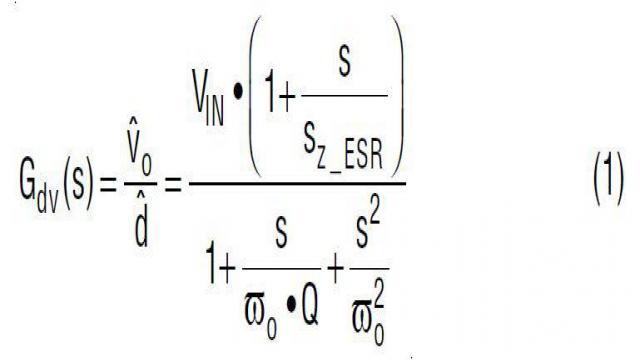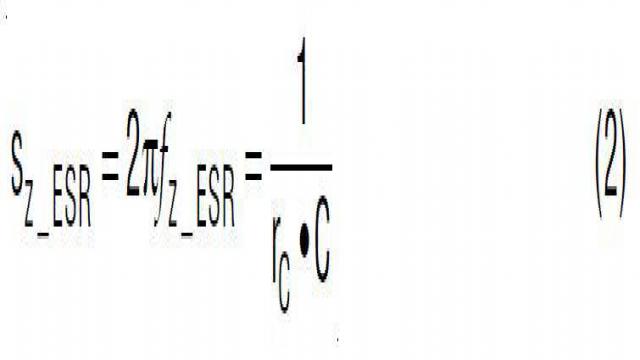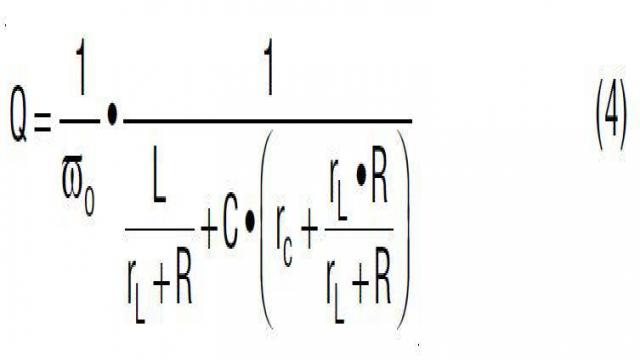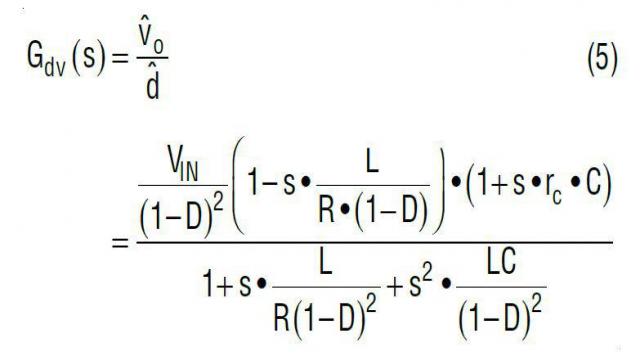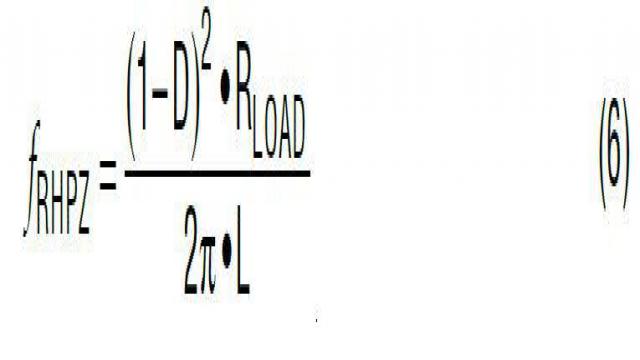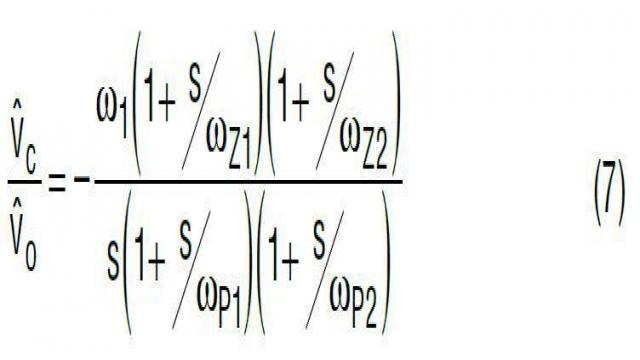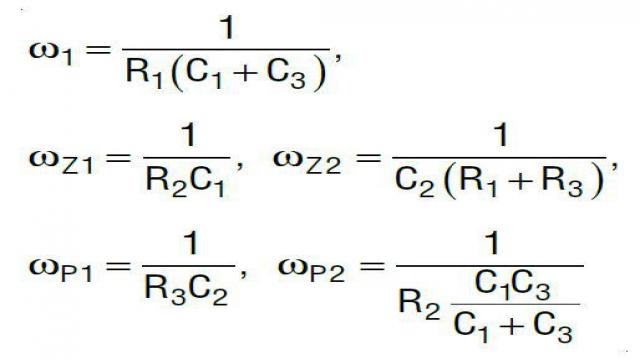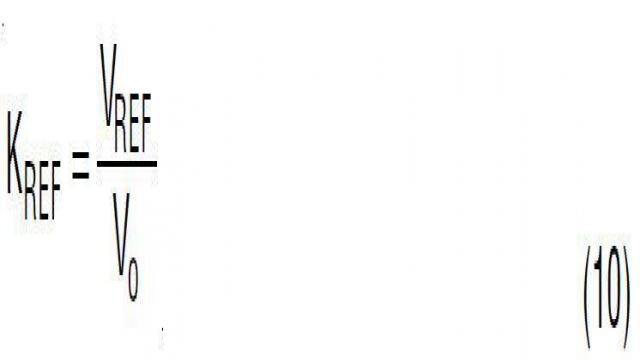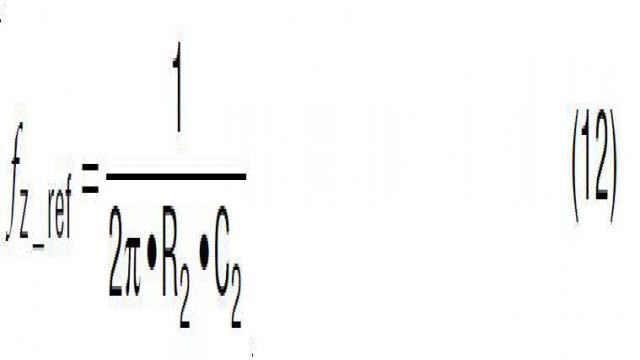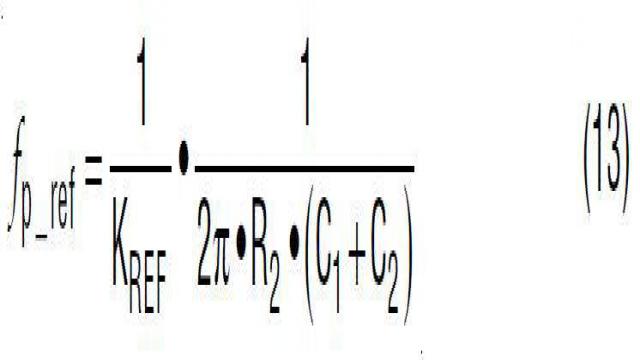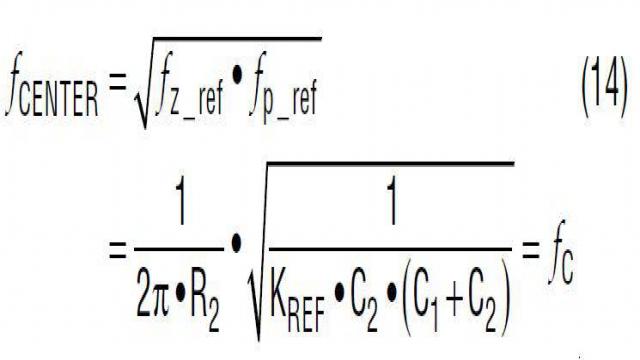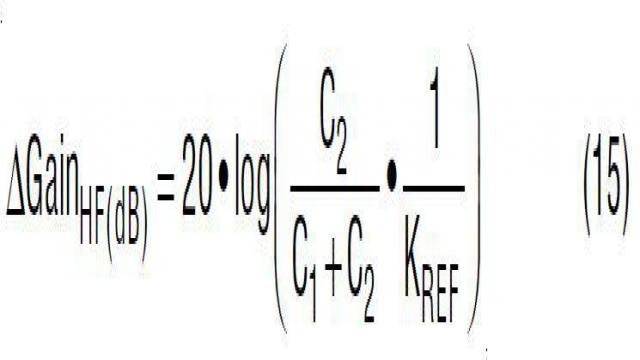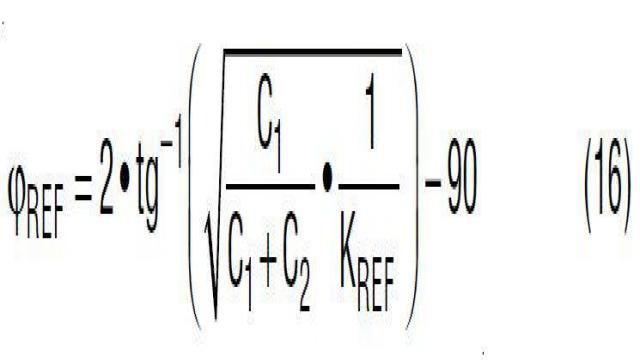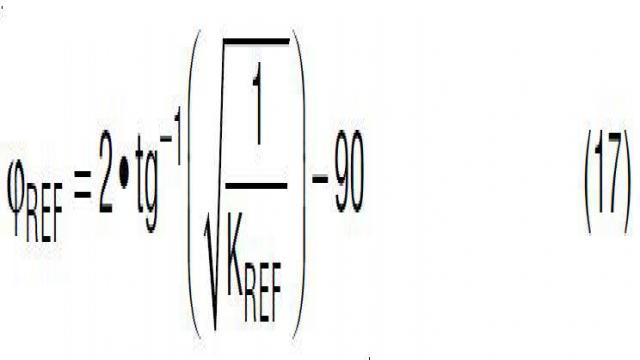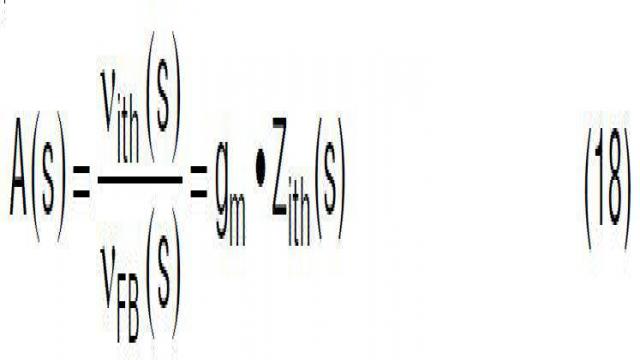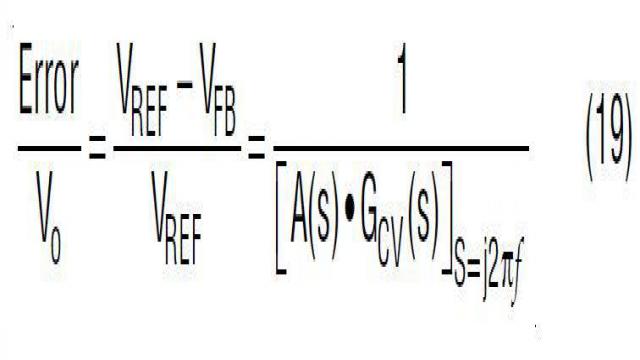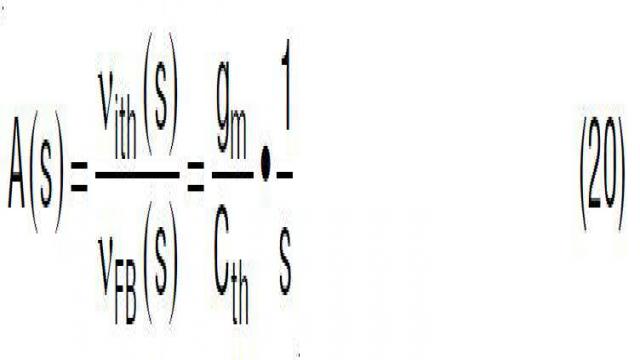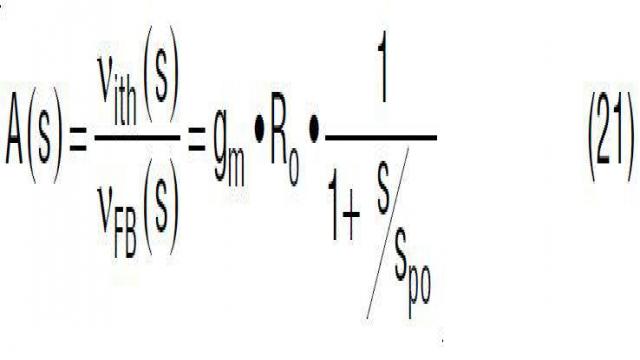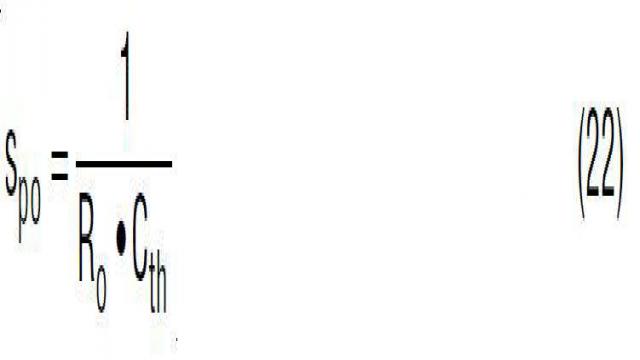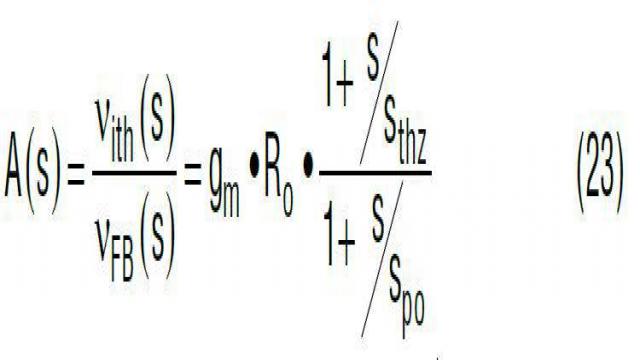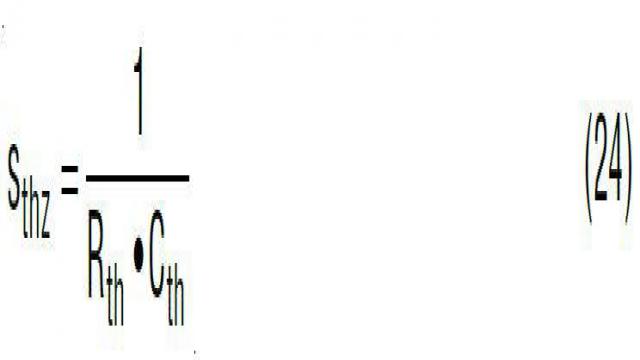引言

如今的电子系统变得越来越复杂，电源轨和电源数量都在不断增加。为了实现最佳电源解决方案密度、可靠性和成本，系统设计师常常需要自己设计电源解决方案，而不是仅仅使用商用砖式电源。设计和优化高性能开关模式电源正在成为越来越频繁、越来越具挑战性的任务。

电源环路补偿设计常常被看作是一项艰难的任务，对经验不足的电源设计师尤其如此。在实际补偿设计中，为了调整补偿组件的值，常常需要进行无数次迭代。对于一个复杂系统而言，这不仅耗费大量时间，而且也不够准确，因为这类系统的电源带宽和稳定性裕度可能受到几种因素的影响。本应用指南针对开关模式电源及其环路补偿设计，说明了小信号建模的基本概念和方法。本文以降压型转换器作为典型例子，但是这些概念也能适用于其他拓扑。本文还介绍了用户易用的 LTpowerCAD™ 设计工具，以减轻设计及优化负担。

确定问题

一个良好设计的开关模式电源 (SMPS) 必须是没有噪声的，无论从电气还是声学角度来看。欠补偿系统可能导致运行不稳定。不稳定电源的典型症状包括：磁性组件或陶瓷电容器产生可听噪声、开关波形中有抖动、输出电压震荡、功率 FET 过热等等。

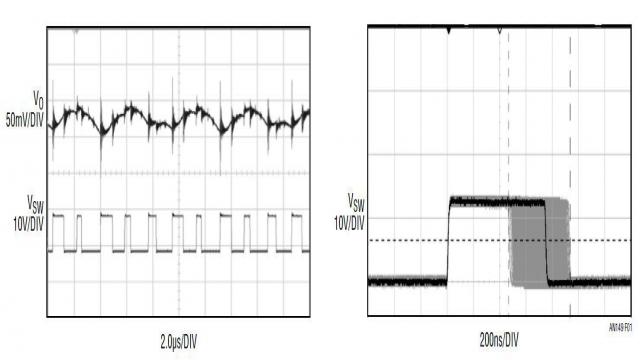
不过，除了环路稳定性，还有很多原因可能导致产生不想要的震荡。不幸的是，对于经验不足的电源设计师而言，这些震荡在示波器上看起来完全相同。即使对于经验丰富的工程师，有时确定引起不稳定性的原因也是很困难。图 1 显示了一个不稳定降压型电源的典型输出和开关节点波形。调节环路补偿可能或不可能解决电源不稳定问题，因为有时震荡是由其他因素引起的，例如 PCB 噪声。如果设计师对各种可能性没有了然于胸，那么确定引起运行噪声的潜藏原因可能耗费大量时间，令人非常沮丧。

图 1：一个 “不稳定” 降压型转换器的典型输出电压和开关节点波形

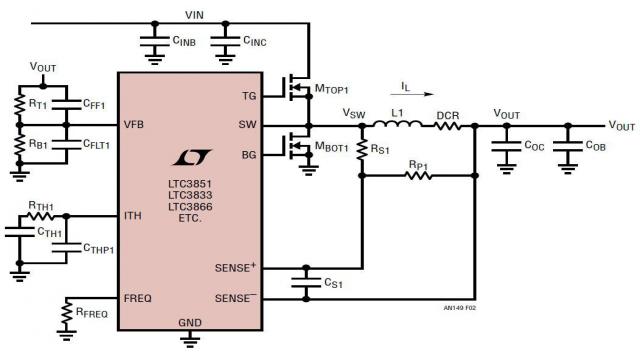
对于开关模式电源转换器而言，例如图 2 所示的 LTC3851 或LTC3833 电流模式降压型电源，一种快速确定运行不稳定是否由环路补偿引起的方法是，在反馈误差放大器输出引脚 (ITH) 和 IC 地之间放置一个 0.1μF 的大型电容器。(或者，就电压模式电源而言，这个电容器可以放置在放大器输出引脚和反馈引脚之间。) 这个 0.1μF 的电容器通常被认为足够大，可以将环路带宽拓展至低频，因此可确保电压环路稳定性。如果用上这个电容器以后，电源变得稳定了，那么问题就有可能用环路补偿解决。

图 2：典型降压型转换器 (LTC3851、LTC3833、LTC3866 等)

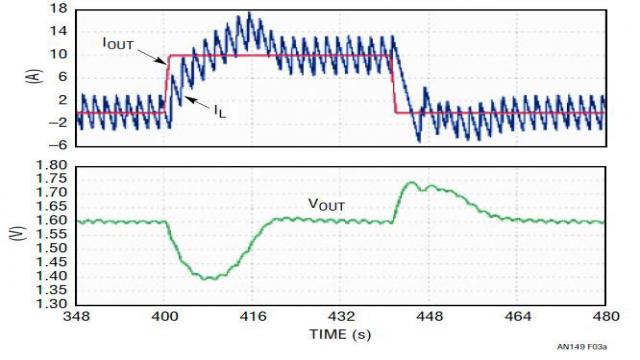
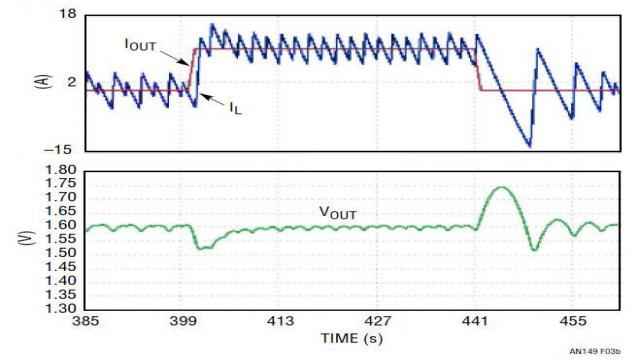
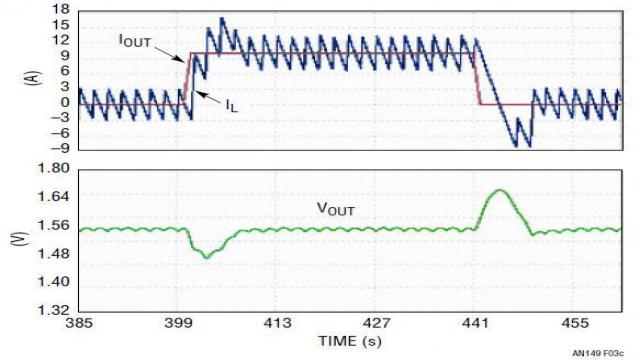
过补偿系统通常是稳定的，但是带宽很小，瞬态响应很慢。这样的设计需要过大的输出电容以满足瞬态调节要求，这增大了电源的总体成本和尺寸。图 3 显示了降压型转换器在负载升高 / 降低瞬态时的典型输出电压和电感器电流波形。图 3a 是稳定但带宽 (BW) 很小的过补偿系统的波形，从波形上能看到，在瞬态时有很大的 VOUT 下冲 / 过冲。图 3b 是大带宽、欠补偿系统的波形，其中 VOUT 的下冲 / 过充小得多，但是波形在稳态时不稳定。图 3c 显示了一个设计良好的电源之负载瞬态波形，该电源具备快速和稳定的环路。

(a) 带宽较小但稳定

(b) 带宽较大但不稳定

(c) 具快速和稳定环路的最佳设计

图 3：典型负载瞬态响应 ━ (a) 过补偿系统；(b) 欠补偿系统；(c) 具快速和稳定环路的最佳设计

PWM 转换器功率级的小信号建模

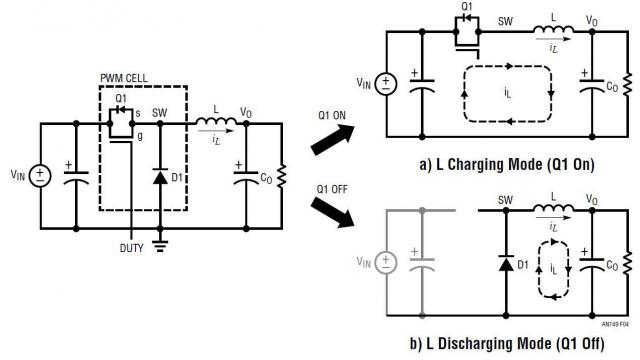
开关模式电源 (SMPS)，例如图 4 中的降压型转换器，通常有两种工作模式，采取哪种工作模式取决于其主控开关的接通 / 断开状态。因此，该电源是一个随时间变化的非线性系统。为了用常规线性控制方法分析和设计补偿电路，人们在 SMPS 电路稳态工作点附近，应用针对 SMPS 电路的线性化方法，开发了一种平均式、小信号线性模型。

图 4：降压型 DC/DC 转换器及其在一个开关周期 TS 内的两种工作模式

建模步骤 1：通过在 TS 平均，变成不随时间变化的系统

所有 SMPS 电源拓扑 (包括降压型、升压型或降压/升压型转换器) 都有一个典型的 3 端子 PWM 开关单元，该单元包括有源控制开关 Q 和无源开关 (二极管) D。为了提高效率，二极管 D 可以用同步 FET 代替，代替以后，仍然是一个无源开关。有源端子 “a” 是有源开关端子。无源端子 “p” 是无源开关端子。在转换器中，端子 a 和端子 p 始终连接到电压源，例如降压型转换器中的 VIN 和地。公共端子 “c” 连接至电流源，在降压型转换器中就是电感器。

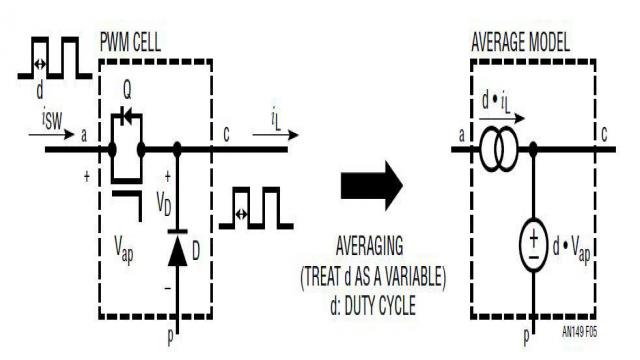
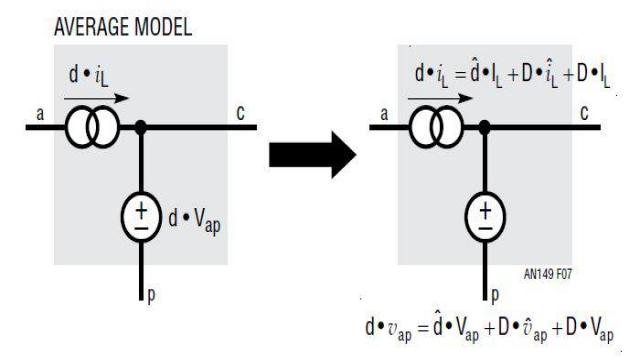
为了将随时间变化的 SMPS 变成不随时间变化的系统，可以通过将有源开关 Q 变成平均式电流源、以及将无源开关 (二极管) D 变成平均式电压源这种方式，应用 3 端子 PWM 单元平均式建模方法。平均式开关 Q 的电流等于 d • iL，而平均式开关 D 的电压等于 d • vap,，如图 5 所示。平均是在一个开关周期 TS 之内进行的。既然电流源和电压源都是两个变量的乘积，那么该系统仍然是非线性系统。

图 5：建模步骤 1：将 3 端子 PWM 开关单元变成平均式电流源和电压源

建模步骤 2：线性AC 小信号建模

下一步是展开变量的乘积以得到线性 AC 小信号模型。例如，变量 ，其中 X 是 DC 稳态的工作点，而  是 AC 小信号围绕 X 的变化。因此，两个变量 x • y 的积可以重写为：

图 6：为线性小信号 AC 部分和 DC 工作点展开两个变量的乘积

图 6 显示，线性小信号 AC 部分可以与 DC 工作点 (OP) 部分分开。两个 AC 小信号变量 的乘积可以忽略，因为这是更加小的变量。按照这一概念，平均式 PWM 开关单元可以重画为如图 7 所示的电路。

图 7：建模步骤 2：通过展开两个变量的乘积给 AC 小信号建模

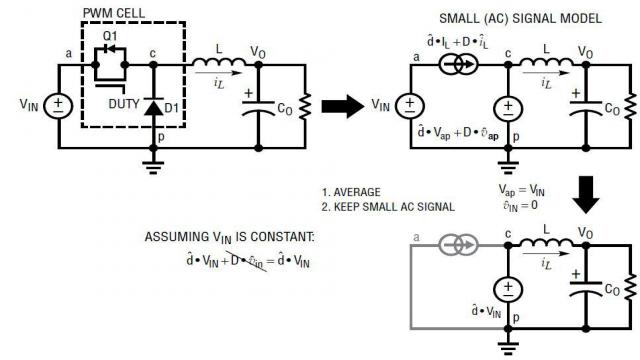
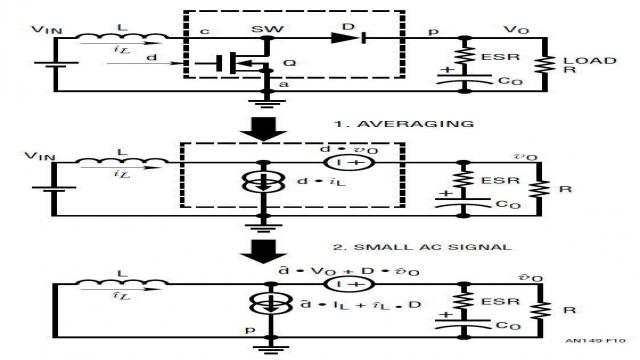
通过将上述两步建模方法应用到降压型转换器上 (如图 8 所示)，该降压型转换器的功率级就可以建模为简单的电压源 ，其后跟随的是一个 L/C 二阶滤波器网络。

图 8：将降压型转换器变成平均式、AC 小信号线性电路

以图 8 所示线性电路为基础，既然控制信号是占空比 d，输出信号是 vOUT，那么在频率域，该降压型转换器就可以用占空比至输出的转移函数 Gdv(s) 来描述：

其中，

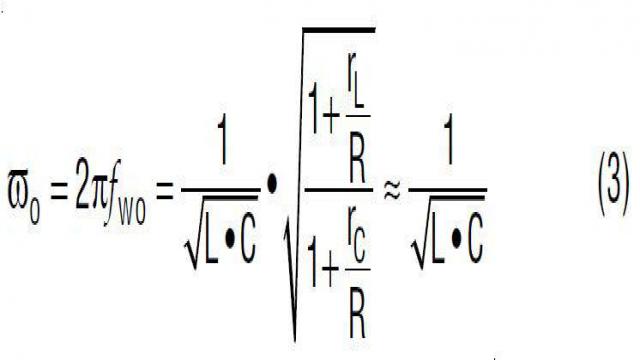
函数 Gdv(s) 显示，该降压型转换器的功率级是一个二阶系统，在频率域有两个极点和一个零点。零点 sZ_ESR 由输出电容器 C 及其 ESR rC 产生。谐振双极点  由输出滤波器电感器 L 和电容器 C 产生。

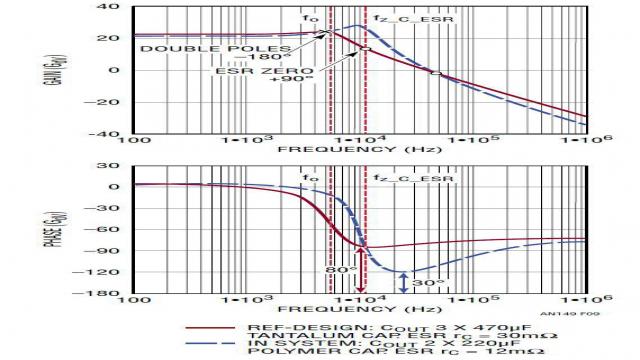
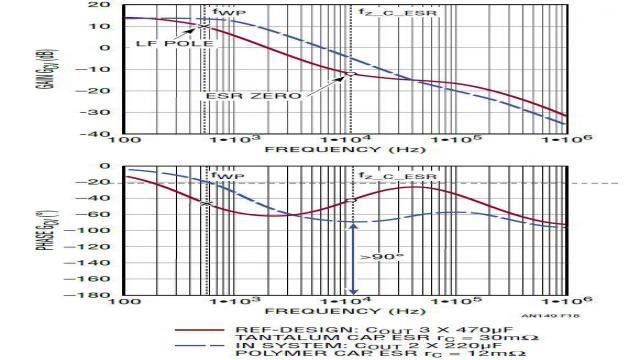
既然极点和零点频率是输出电容器及其 ESR 的函数，那么函数 Gdv(s) 的波德图随所选择电源输出电容器的不同而变化，如图 9 所示。输出电容器的选择对该降压型转换器功率级的小信号特性影响很大。如果该电源使用小型输出电容或 ESR 非常低的输出电容器，那么 ESR 零点频率就可能远远高于谐振极点频率。功率级相位延迟可能接近 –180°。结果，当负压反馈环路闭合时，可能很难补偿该环路。

图 9：COUT 电容器变化导致功率级 Gdv(s) 相位显著变化

升压型转换器的小信号模型

利用同样的 3 端子 PWM 开关单元平均式小信号建模方法，也可以为升压型转换器建模。图 10 显示了怎样为升压型转换器建模，并将其转换为线性 AC 小信号模型电路。

图 10：升压型转换器的 AC 小信号建模电路

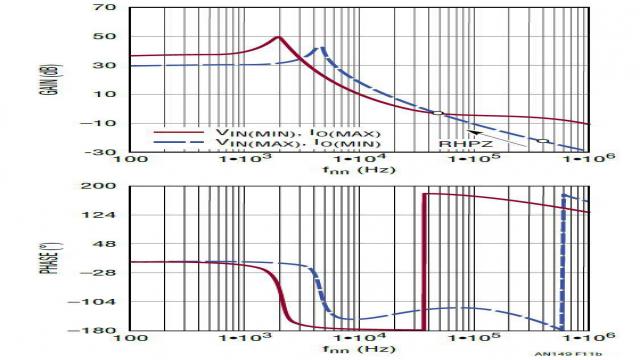
升压型转换器功率级的转移函数 Gdv(s) 可从等式 5 中得出。它也是一个二阶系统，具有 L/C 谐振。与降压型转换器不同，升压型转换器除了 COUT ESR 零点，还有一个右半平面零点 (RHPZ) 。该 RHPZ 导致增益升高，但是相位减小 (变负)。等式 6 也显示，这个 RHPZ 随占空比和负载电阻不同而变化。既然占空比是 VIN 的函数，那么升压型转换器功率级的转移函数 Gdv(s) 就随 VIN 和负载电流而变。在低 VIN 和大负载 IOUT_MAX 时，RHPZ 位于最低频率处，并导致显著的相位滞后。这就使得难以设计带宽很大的升压型转换器。作为一个一般的设计原则，为了确保环路稳定性，人们设计升压型转换器时，限定其带宽低于其最低 RHPZ 频率的 1/10。其他几种拓扑，例如正至负降压 / 升压、反激式 (隔离型降压 / 升压)、SEPIC 和 CUK 转换器，所有都存在不想要的 RHPZ，都不能设计成带宽很大、瞬态响应很快的解决方案。

 

图 11：升压型转换器功率级小信号占空比至 VO 转移函数随 VIN 和负载而改变

用电压模式控制闭合反馈环路

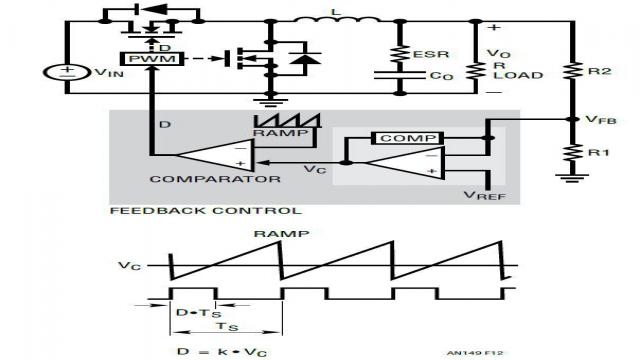
输出电压可以由闭合的反馈环路系统调节。例如，在图 12 中，当输出电压 VOUT 上升时，反馈电压 VFB 上升，负反馈误差放大器的输出下降，因此占空比 d 下降。结果，VOUT 被拉低，以使 VFB = VREF。误差运算放大器的补偿网络可以是 I 型、II 型或 III 型反馈放大器网络。只有一个控制环路调节 VOUT。这种控制方法称为电压模式控制。凌力尔特公司的 LTC3861 和 LTC3882 就是典型的电压模式降压型控制器。

图 12：具闭合电压反馈环路的电压模式降压型转换器方框图

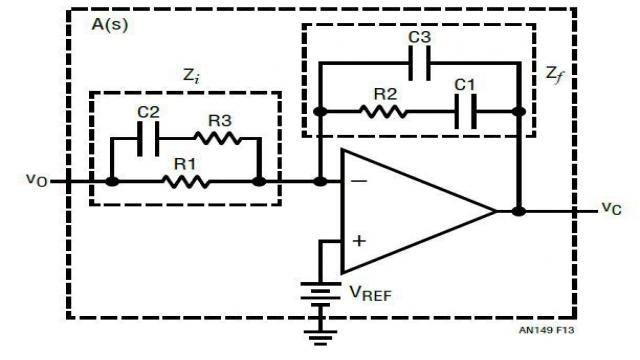
为了优化电压模式 PWM 转换器，如图 13 所示，通常需要一种复杂的 III 型补偿网络，以凭借充足的相位裕度设计一个快速环路。如等式 7 和图 14 所示，这种补偿网络在频率域有 3 个极点和两个零点：低频积分极点 (1/s) 提供高的 DC 增益，以最大限度减小 DC 调节误差，两个零点放置在系统谐振频率 f0 附近，以补偿由功率级的 L 和 C 引起的 –180° 相位延迟，在 fESR 处放置第一个高频极点，以消除 COUT ESR 零点，第二个高频极点放置在想要的带宽 fC 以外，以衰减反馈环路中的开关噪声。III 型补偿相当复杂，因为这种补偿需要 6 个 R/C 值。找到这些值的最佳组合是个非常耗时的任务。

图 13：用于电压模式转换器的 III 型反馈补偿网络

其中

图 14：III 型补偿 A(s) 提供 3 个极点和两个零点，以实现最佳的总体环路增益 TV(s)

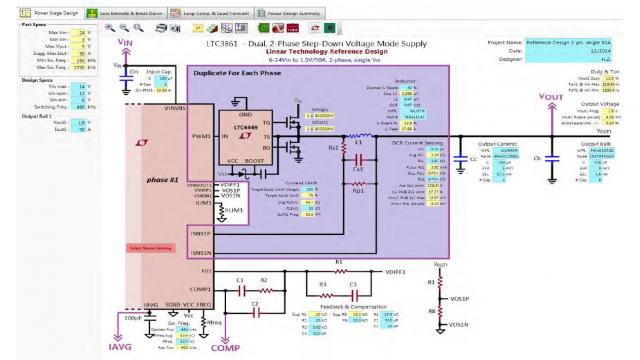
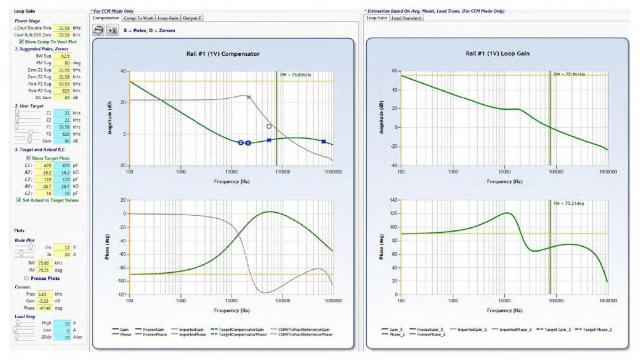
为了简化和自动化开关模式电源设计，凌力尔特开发了 LTpowerCAD 设计工具。这工具使环路补偿设计任务变得简单多了。LTpowerCAD 是一款可在 www.linear.com.cn/LTpowerCAD 免费下载的设计工具。该软件帮助用户选择电源解决方案、设计功率级组件以及优化电源效率和环路补偿。如图 15 例子所示，就给定的凌力尔特电压模式控制器而言 (例如 LTC3861)，其环路参数可用该设计工具建模。对于一个给定的功率级，用户可以确定极点和零点位置 (频率)，然后按照该软件的指导，带入真实的 R/C 值，实时检查总体环路增益和负载瞬态性能。之后，设计方案还可以输出到一个 LTspice® 仿真电路上，进行实时仿真。

(a) LTpowerCAD 功率级设计页面

(b) LTpowerCAD 环路补偿和负载瞬态设计页面

图 15：LTpowerCAD 设计工具减轻了电压模式转换器 III 型环路设计的负担

(从 www.linear.com.cn/LTpowerCAD 免费下载)

为电流模式控制增加电流环路

单一环路电压模式控制受到一些限制。这种模式需要相当复杂的 III 型补偿网络。环路性能可能随输出电容器参数及寄生性变化而出现大幅改化，尤其是电容器 ESR 和 PCB 走线阻抗。一个可靠的电源还需要快速过流保护，这就需要一种快速电流检测方法和快速保护比较器。对于需要很多相位并联的大电流解决方案而言，还需要一个额外的电流均分网络 / 环路。

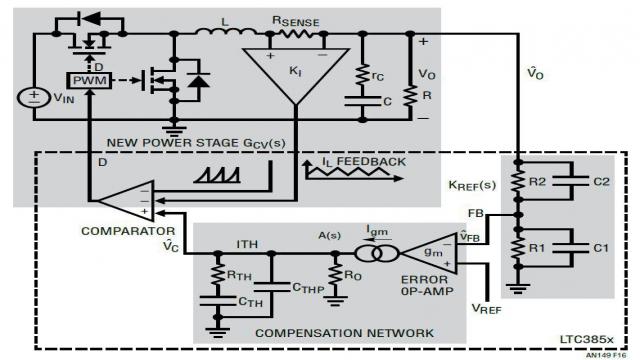
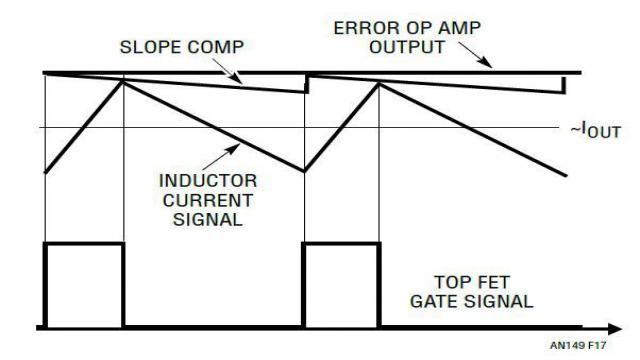
给电压模式转换器增加一个内部电流检测通路和反馈环路，使其变成一个电流模式控制的转换器。图 16 和 17 显示了典型峰值电流模式降压型转换器及其工作方式。内部时钟接通顶端的控制 FET。之后，只要所检测的峰值电感器电流信号达到放大器 ITH 引脚电压 VC，顶端的 FET 就断开。从概念上来看，电流环路使电感器成为一个受控电流源。因此，具闭合电流环路的功率级变成了 1 阶系统，而不是具 L/C 谐振的 2 阶系统。结果，功率级极点引起的相位滞后从 180° 减少为约 90°。相位延迟减少使补偿外部电压环路变得容易多了。相位延迟减少还降低了电源对输出电容器或电感变化的敏感度，如图 18 所示。

图 16：具内部电流环路和外部电压反馈环路的电流模式转换器方框图

图 17：峰值电流模式控制信号波形

图 18：具闭合电流环路的新功率级转移函数 GCV(s)

电感器电流信号可以直接用一个附加的 RSENSE 检测，或者间接地通过电感器绕组 DCR 或 FET RDS(ON) 检测。电流模式控制还提供其他几项重要的好处。如图 17 所示，既然电感器电流以逐周期方式、通过放大器输出电压检测和限制，那么系统在过载或电感器电流饱和时，就能够更准确和更快速地限制电流。在加电或输入电压瞬态时，电感器浪涌电流也受到了严格控制。当多个转换器 / 相位并联时，通过将放大器 ITH 引脚连到一起，凭借电流模式控制，可以在多个电源之间非常容易地均分电流，从而实现了一个可靠的多项 (PolyPhase®) 设计。典型电流模式控制器包括凌力尔特公司的 LTC3851A、LTC3833 和 LTC3855 等。

峰值与谷值电流模式控制方法

图 16 和 17 所示的电流模式控制方法是峰值电感器电流模式控制。转换器以固定开关频率 fSW 工作，从而非常容易实现时钟同步和相位交错，尤其是对于并联转换器。然而，如果在控制 FET 栅极关断后，紧接着就发生负载升压瞬态，那么转换器就必须等待一段时间，这段时间等于 FET 断开时间 TOFF，直到下一个时钟周期响应该瞬态为止。这个 TOFF 延迟通常不是问题，但是对于一个真正的快速瞬态系统，它却很重要。此外，控制 FET 的最短接通时间 (TON_min) 不可能非常短，因为电流比较器需要噪声消隐时间以避免错误触发。对于高 VIN/VOUT 降压比应用而言，这限制了最高开关频率 fSW。此外，峰值电流模式控制还需要一定的斜率补偿，以在占空比超过 50% 时保持电流环路稳定。对于凌力尔特公司的控制器而言，这不是个问题。凌力尔特的控制器通常有内置自适应斜率补偿，以在整个占空比范围内确保电流环路稳定性。LTC3851A 和 LTC3855 是典型的峰值电流模式控制器。

谷值电流模式控制器产生受控 FET 接通时间，并一直等待直到电感器谷值电流达到其谷值限制 (VITH) 以才再次接通控制 FET。因此，电源可以在控制 FET 的 TOFF 时间响应负载升高瞬态。此外，既然接通时间是固定的，那么控制 FET 的 TON_min 可以比峰值电流模式控制时短，以允许更高的 fSW，实现高降压比应用。谷值电流模式控制不需要额外的斜率补偿就能实现电流环路稳定性。然而，使用谷值电流模式控制时，因为允许开关周期 TS 变化，所以在示波器上，开关节点波形可能出现更大的抖动。LTC3833 和 LTC3838 是典型的谷值电流模式控制器。

为具备闭合电流环路的新功率级建模

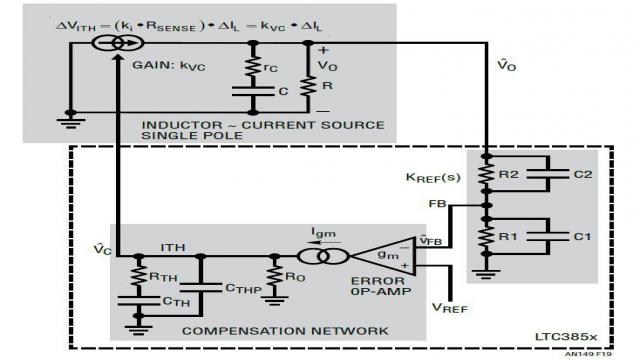
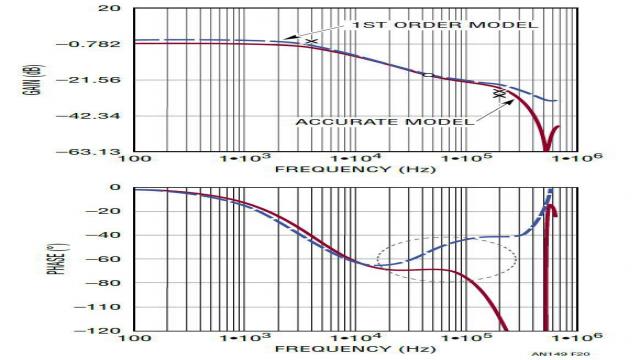
图 19 显示，通过仅将电感器作为受放大器 ITH 引脚电压  控制的电流源，产生了一个简化、具内部电流环路的降压型转换器功率级的一阶模型。类似方法也可用于其他具电感器电流模式控制的拓扑。这个简单的模型有多好? 图 20 显示了该一阶模型和一个更复杂但准确的模型之间转移函数 GCV(s) = vOUT/vC 的比较结果。这是一个以 500kHz 开关频率运行的电流模式降压型转换器。在这个例子中，一阶模型直到 10kHz 都是准确的，约为开关频率 fSW 的 1/50。之后，一阶模型的相位曲线就不再准确了。因此这个简化的模型仅对于带宽较小的设计才好用。

图 19：电流模式降压型转换器的简单一阶模型

图 20：电流模式降压型转换器的一阶模型和准确模型之间的 GCV(s) 比较

实际上，针对电流模式转换器，在整个频率范围内开发一个准确的小信号模型相当复杂。R. Ridley的电流模式模型 [3] 在电源行业是最流行的一种模型，用于峰值电流模式和谷值电流模式控制。最近，Jian Li 为电流模式控制开发了一种更加直观的电路模型 [4]，该模型也可用于其他电流模式控制方法。为了简便易用，LTpowerCAD 设计工具实现了这些准确模型，因此，即使一位经验不足的用户，对 Ridley 或 Jian Li 的模型没有太多了解，也可以非常容易地设计一个电流模式电源。

电流模式转换器的环路补偿设计

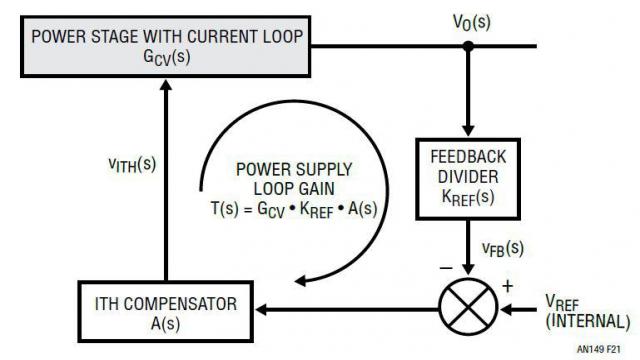
在图 16 和图 21 中，具闭合电流环路的功率级 Gcv(s) 由功率级组件的选择决定，主要由电源的 DC 规格 / 性能决定。外部电压环路增益 T(s) = GCV(s) • A(s) • KREF(s) 因此由电压反馈级 KREF(s) 和补偿级 A(s) 决定。这两个级的设计将极大地决定电源的稳定性和瞬态响应。

图 21：反馈环路设计的控制方框图

总之，闭合电压环路 T(s) 的性能由两个重要参数决定：环路带宽和环路稳定性裕度。环路带宽由交叉频率 fC 量化，在这一频点上，环路增益 T(s) 等于1 (0dB)。环路稳定性裕度一般由相位裕度或增益裕度量化。环路相位裕度  的定义是在交叉频率点上总体 T(s) 相位延迟和 –180° 之差。通常需要 45° 或 60° 最小相位裕度以确保稳定性。对于电流模式控制而言，为了衰减电流环路中的开关噪声，环路增益裕度定义为在 ½ • fSW 处的衰减。一般而言，希望在 ½ • fSW 处有最小 8dB 衰减 (-8dB 环路增益)。

选择想要的电压环路交叉频率 fC

更大的带宽有助于实现更快的瞬态响应。不过，增大带宽通常会降低稳定性裕度，使控制环路对开关噪声更加敏感。一个最佳设计通常在带宽 (瞬态响应) 和稳定性裕度之间实现了良好的平衡。实际上，电流模式控制还通过在 1/2 • fSW 处电流信号的采样效应 [3]，而引入了一对双极点 。这些双极点在 ½ • fSW 附近引入了不想要的相位延迟。一般而言，要获得充足的相位裕度并充分衰减 PCB 噪声，交叉频率就要选为低于相位开关频率 fSW 的 1/10 至 1/6。

用 R1、R2、C1 和 C2 设计反馈分压器网络 Kref(s)

在图 16 中，DC 增益 KREF 的 Kref(s) 是内部基准电压 VREF 和想要的 DC 输出电压 Vo 之比。电阻器 R1 和 R2 用来设定想要的输出 DC 电压。

其中

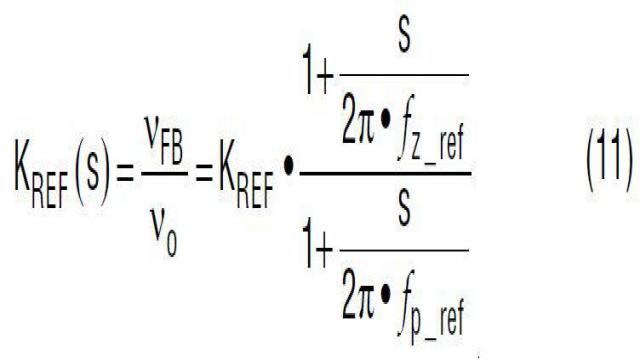
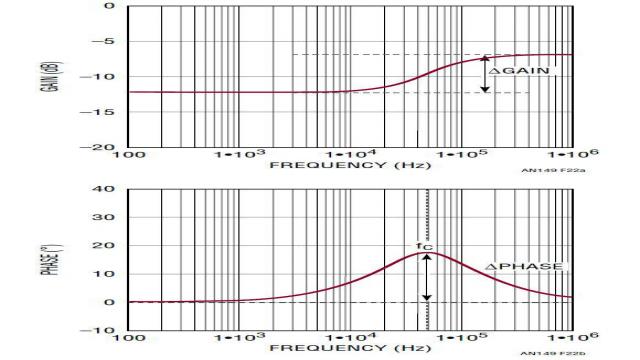
可以增加可选电容器 C2，以改进反馈环路的动态响应。从概念上来说，在高频时，C2 为输出 AC 电压信号提供低阻抗前馈通路，因此，加速了瞬态响应。但是 C2 还有可能给控制环路带来不想要的开关噪声。因此，可以增加一个可选 C1 滤波器电容器，以衰减开关噪声。如等式 11 所示，包括 C1 和 C2 的总体电阻器分压器转移函数 KREF(s) 有一个零点和一个极点。图 22 显示了 KREF(s) 的波德图。通过设计成 fz_ref < fp_ref，C1 和 C2 与 R1 和 R2 一起，导致在以 fCENTER 为中心的频带中相位增大，相位增大量在等式 14 中给出。如果 fCENTER 放置在目标交叉频率 fC 处，那么 Kref(s) 使相位超前于电压环路，提高了相位裕度。另一方面，图 22 还显示，C1 和 C2 提高了高频时的分压器增益。这种情况是不想要的，因为高频增益提高使控制环路对开关噪声更加敏感。C1 和 C2 导致的高频增益提高在等式 15 中给出。

其中

和

图 22：电阻器分压器增益 KREF(s) 的转移函数波德图

就给定的 C1 和 C2 而言，分压器网络导致的相位增大量 φREF 可以用等式 16 计算。此外，在 C2 >> C1 的情况下，就给定输出电压而言，最大相位增大量由等式 17 给出。从该等式中也可以看出，最大相位增大量 φREF_max 由分比 KREF = VREF/VO 决定。既然 VREF 就给定控制器而言是固定的，那么用更高的输出电压 VO 可以得到更大的相位增大量。

选择φREF、C1 和 C2 时，需要在想要的相位增大量与不想要的高频增益提高量之间做出权衡。之后，需要检查总体环路增益以实现最佳值。

设计电压环路 ITH 误差放大器的 II 型补偿网络

ITH 补偿 A(s) 是环路补偿设计中最关键的一步，因为这一步决定 DC 增益、交叉频率 (带宽) 和电源电压环路的相位 / 增益裕度。就一个电流源输出、gm 跨导型放大器而言，其转移函数 A(s) 由等式 18 给出：

其中，gm 是跨导误差放大器的增益。Zith(s) 是放大器输出 ITH 引脚上补偿网络的阻抗。

从图 21 所示的控制方框图中可以看出，电压环路调节误差可由以下等式量化：

因此，为了最大限度降低 DC 调节误差，大的 DC 增益 A(s) 是非常想要的。为了最大限度提高 DC 增益 A(s)，首先要将电容器 Cth 放在放大器输出 ITH 引脚处以形成一个积分器。在这种情况下，A(s) 传输增益为：

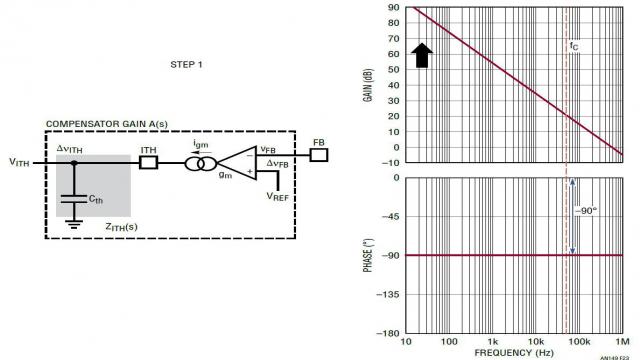
图 23 显示了 A(s) 的原理图及其波德图。如图所示，电容器 Cth 以无限高的 DC增益在 A(s) 中产生了一个积分项。不幸的是，除了初始的 –180° 负反馈，Cth 又增加了 –90° 的相位滞后。将一阶系统功率级 GCV(s) 的  –90° 相位包括进来以后，在交叉频率 fC 处的总体电压环路相位接近 –360°，该环路接近不稳定状态。

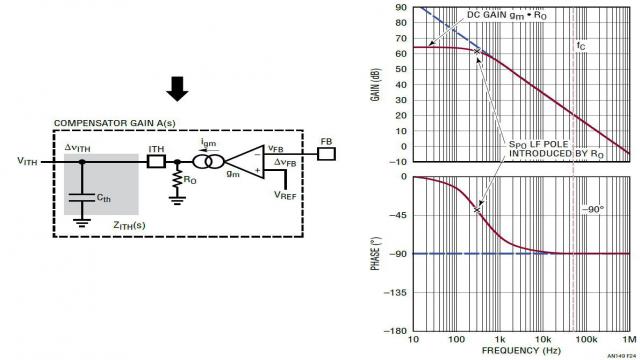
实际上，电流源 gm 放大器的输出阻抗不是一个无限大的值。在图 24 中，Ro 是 gm 放大器 ITH 引脚的内部输出阻抗。凌力尔特公司控制器的 Ro 通常较高，在 500kΩ 至 1MΩ 范围。因此，单个电容器的 A(s) 转移函数变成了等式 21。该转移函数有一个低频极点 fpo (由 RO · Cth 决定)。因此 A(s) 的 DC 增益实际上是 gm · RO。如图 24 所示，在预期的交叉频率 fc_exp 处，A(s) 仍然有 –90° 的相位滞后。

其中

图 23：步骤 1：简单的电容器补偿网络 A(s) 及其波德图

图 24：包括 gm 放大器输出阻抗 RO 的单极点 A(s) 

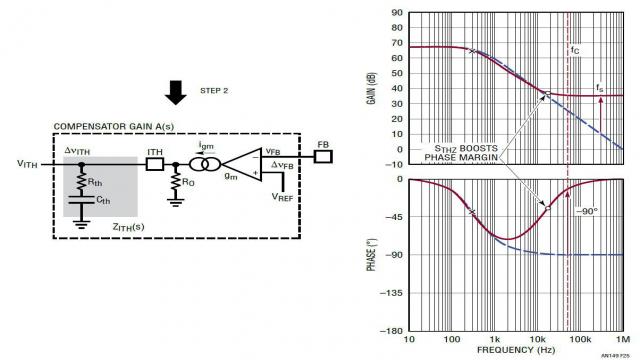
为了提高 fC 处的相位，增加一个与 Cth 串联的电阻器 Rth 以产生一个零点，如等式 23 和图 25 所示。该零点贡献高至 +90° 超前相位。如图 25 所示，如果零点 sthz 放置在交叉频率 fC 之前，那么 A(s) 在 fC 处的相位可以显着地增大。因此，这样做提高了电压环路的相位裕度。

其中

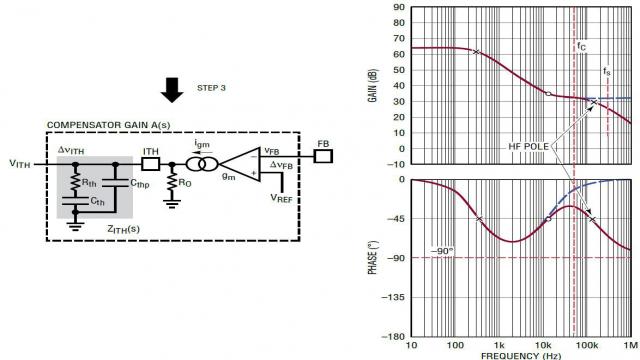
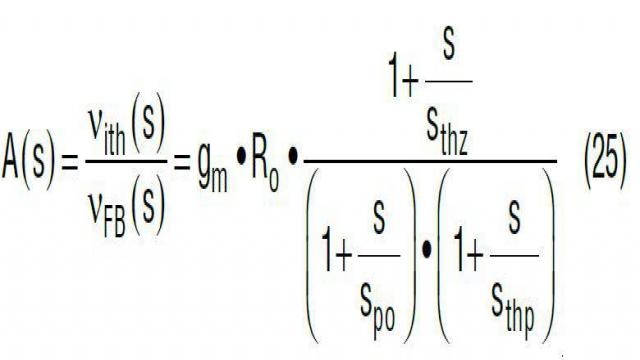
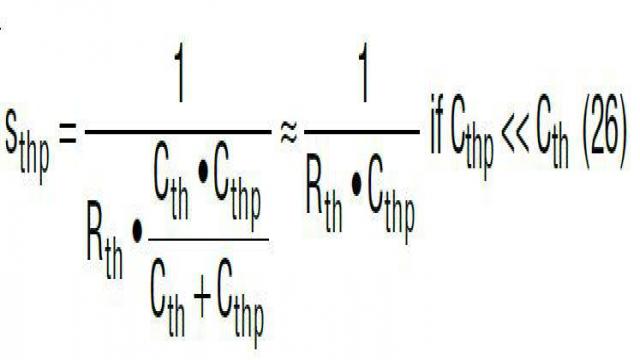
不幸的是，增加这个零点 sthz 也有害处，增益 A(s) 在 fC 以外的高频范围内显着地提高。因此，由于在开关频率处 A(s) 衰减较少，所以开关噪声更有可能进入控制环路。为了补偿这一增益提高并衰减 PCB 噪声，在 ITH 引脚至 IC 信号地之间有必要增加另一个小型陶瓷电容器 Cthp，如图 26 所示。一般情况下，选择 Cthp << Cth。在 PCB 布局中，滤波器电容器 Cthp 应该放置在尽可能靠近 ITH 引脚的地方。通过增加 Cthp，最终补偿转移函数 A(s) 由等式 25 和 26 给出，其波德图如图 26 所示。Cthp 引入一个高频极点 sthp，该极点应该位于交叉频率 fC 和开关频率 fS 之间。Cthp 降低了 fS 处的 A(s) 增益，但是也有可能减小 fC 的相位。sthp 的位置是相位裕度和电源 PCB 抗噪声性能之间权衡的结果。

图 25：步骤 2：增加 RTH 零点以增大相位 —— 单极点、单零点补偿 A(s)

图 26：步骤 3：增加高频去耦 Cthp —— 双极点、单零点补偿 A(s)

其中

既然电流模式功率级是一个准单极点系统，那么图 26 所示的双极点和单零点补偿网络一般足够提供所需的相位裕度了。

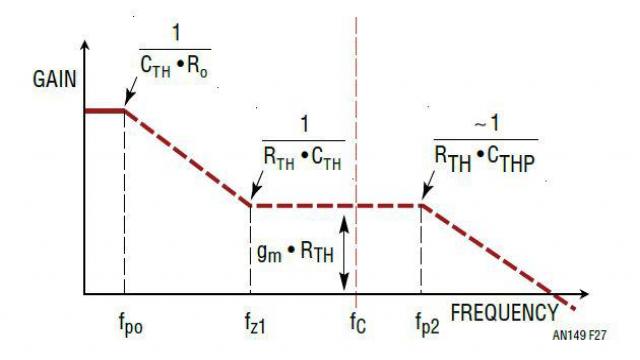
放大器 ITH 引脚上这个双极点、单零点补偿网络也称为 II 型补偿网络。总之，有两个电容器 CTH 和 CTHP 和一个电阻器 RTH。这个 R/C 网络与放大器输出电阻 Ro 一起，产生了一个如图 27 所示的典型转移函数，一个零点位于 fz1 处，两个极点位于 fpo 和 fp2 处。

图 27：II 型补偿网络转移函数的概念图

补偿 R/C 值与负载阶跃瞬态响应

前一节讲述了 II 型补偿网络在频率域的表现。在一个闭合环路电源设计中，一个重要的性能参数是负载升高 (负载下降) 瞬态时电源的输出电压下冲 (或过充)，这个参数通常直接受环路补偿设计的影响。

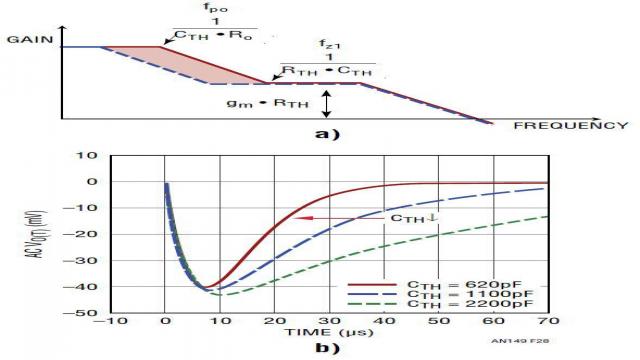
1）CTH 对负载阶跃瞬态的影响。CTH 影响低频极点 fpo 和零点 fz1 的位置。如图 28 所示，CTH 越小，转移函数 A(s) 的低至中频增益能越高。结果，这有可能缩短负载瞬态响应达到稳定的时间，而对 VOUT 下冲 (或过冲) 幅度没有很大影响。另一方面，CTH 越小，意味着 fz1 频率越高。这有可能在目标交叉频率 fC 处因 fz1 升高而减少增加的相位。

图 28：CTH 对转移函数和负载瞬态的影响

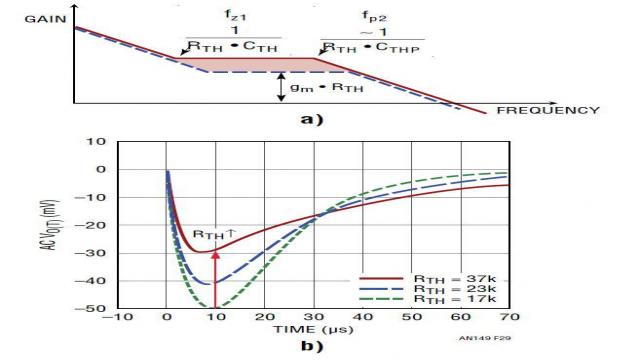
2）RTH 对负载阶跃瞬态的影响。图 29 显示，RTH 影响零点 fz1 和极点 fp2 的位置。更重要的是，RTH 越大，fz1 和 fp2 之间的 A(s) 增益就越高。因此 RTH 增大会直接提高电源带宽 fc，并在负载瞬态时降低 VOUT 的下冲 / 过冲。然而，如果 RTH 太大，电源带宽 fc 可能过高，相位裕度就不够了。

图 29：RTH 对转移函数和负载瞬态的影响

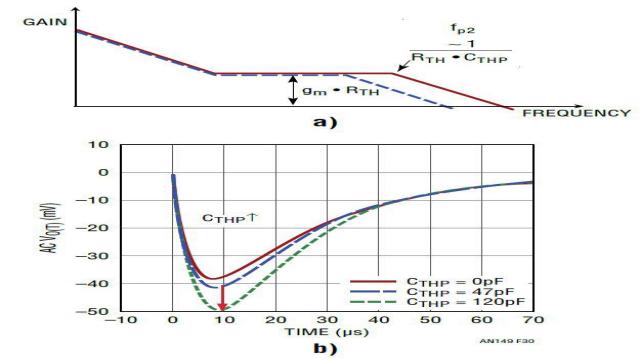
3) CTHP 对负载阶跃瞬态的影响。图 30 显示，CTHP 影响极点 fp2 的位置。CTHP 用作去耦电容器，降低 ITH 引脚的开关噪声，以最大限度减小开关抖动。如果电源带宽 fc > fp2，那么 CTHP 对负载瞬态影响就不太大。如果 CTHP 设计过度，导致 fp2 靠近 fc，那么它就可能减小带宽和相位裕度，导致瞬态下冲 / 过冲增大。

图 30：CTHP 对转移函数和负载瞬态的影响

用 LTpowerCAD 设计工具设计一个电流模式电源

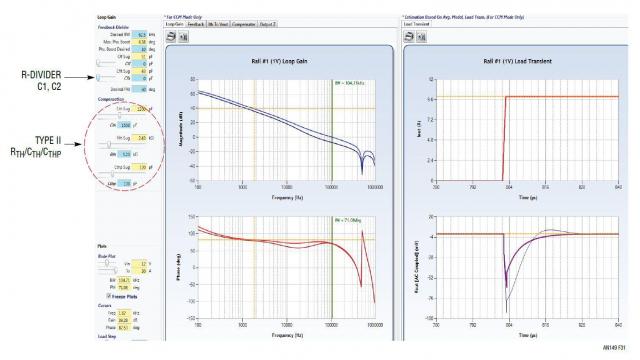
通过 LTpowerCAD 设计工具，用户可以非常容易地设计和优化凌力尔特电流模式电源的环路补偿及负载瞬态性能。很多凌力尔特产品都可用其环路参数准确地建模。首先，用户需要先设计功率级，在这一步，他们需要设计电流检测网络，确保为 IC 提供足够的 AC 检测信号。之后，在环路设计页面，用户可以通过简便地移动滑动条，观察总体环路带宽、相位裕度和相应的负载瞬态性能，依此调节环路补偿 R/C 值。就一个降压型转换器而言，用户通常需要设计低于 1/6 fSW 的带宽，有至少 45° (或 60°) 的相位裕度，在 ½ fSW 处至少有 8dB 的总体环路增益衰减。就一个升压型转换器而言，由于存在右半平面零点 (RHPZ)，所以用户需要设计低于最差情况 RHPZ 频率 1/10 的电源带宽。LTpowerCAD 设计文件可以输出到 LTspice 进行实时仿真，以检查详细的电源动态性能，例如负载瞬态、加电 / 断电、过流保护 … 等等。

图 31：LTpowerCAD 设计工具减轻了环路补偿设计和瞬态优化负担

测量电源环路增益

LTpowerCAD 和 LTspice 程序不是用来取代真实电源的最终工作台环路增益测量。在将设计投入最终生产之前，总是有必要进行测量。尽管电源模型理论上是正确，但是这些模型不可能全面考虑到电路寄生性和组件非线性，例如输出电容器的 ESR 变化、电感器和电容器的非线性 … 等等。另外，电路 PCB 噪声和有限的测量准确度还可能引起测量误差。这就是为什么有时理论模型和测量结果可能相差很大的原因。如果发生这种情况，负载瞬态测试就可以用来进一步确认环路稳定性。

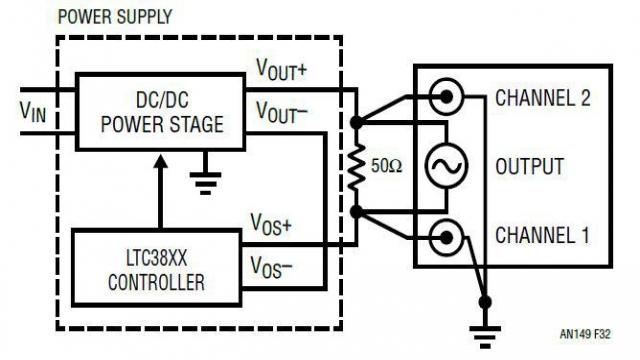
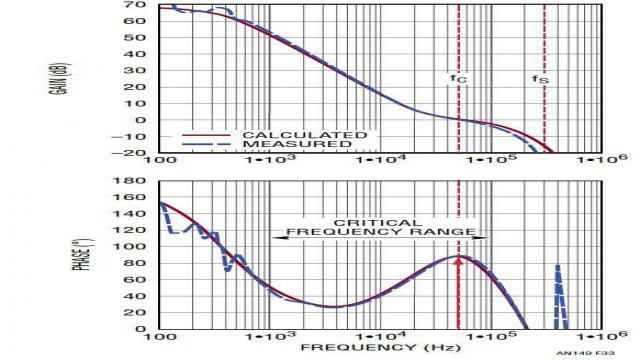
图 32 显示了用频率分析仪系统测量一个非隔离式电源的典型电源环路增益的测量配置。为了测量环路增益，在电压反馈环路中插入了一个 50Ω 至 100Ω 的电阻，并给这个电阻器加上了一个 50mV 隔离式 AC 信号。通道 2 连接到输出电压，通道 1 连接到这个电阻器的另一侧。环路增益由频率分析仪系统通过 Ch2/Ch1 计算。图 33 显示了测得的和 LTpowerCAD 计算得出的典型电流模式电源 LTC3851A 之环路波德图。在关键的 1kHz 至 100kHz 频率范围内，两条曲线吻合得非常好。

图 32：测量电源环路增益的测试配置

图 33：测得的和 LTpowerCAD 建模得到的电流模式降压型转换器之环路增益

其他导致不稳定性的因素

工作条件：

如果在示波器上电源开关或输出电压波形看起来不稳定或有抖动，那么首先，用户需要确保电源是在稳态条件下工作的，没有负载或输入电压瞬态。对于非常小或非常大的占空比应用而言，如果进入脉冲跳跃工作模式，就要检查是否达到了最短接通时间或断开时间限制。对于需要外部同步信号的电源而言，要确保信号干净并位于控制器数据表给定的线性范围之内。有时还有必要调整锁相环 (PLL) 滤波器网络。

电流检测信号和噪声：

在电流模式电源中，为了最大限度地降低检测电阻器的功率损耗，最大电流检测电压一般非常低。例如，LTC3851A 可能有 50mV 最大检测电压。PCB 噪声有可能干扰电流检测环路，并导致开关表现不稳定。为了通过调试以确定是否确实是环路补偿问题，可以在 ITH 引脚到 IC 地之间放置一个大型 0.1µF 电容器。如果有了这个电容器电源仍然不稳定，那么下一步就是检查设计方案。一般而言，电感器和电流检测网络应该设计成，在 IC 电流检测引脚上至少有 10mV 至 15mV 峰值至峰值 AC 电感器电流信号。另外，电流检测走线可以用一对扭绞跨接线重新布设，以检查这样是否能解决问题。

对于 PCB 布局而言，有一些重要考虑因素 [6]。总之，通常需要用一对紧挨着布设、返回 SENSE+ 和 SENSE- 引脚的电流检测走线实现开尔文检测。如果某个 PCB 通孔用在 SENSE- 网中，那么要确保这个通孔不接触到其他 VOUT 平面。跨接 SENSE+ 和 SENSE- 的滤波器电容器应该通过直接走线连接，放置在尽可能靠近 IC 引脚的地方。有时需要滤波器电阻器，而且这些电阻器也必须靠近 IC。

控制芯片组件放置与布局：

控制 IC 周围组件的放置和布局也是至关重要的 [6]。如果可能，所有陶瓷去耦电容器都应该靠近其引脚。尤其重要的是，ITH 引脚电容器 Cthp 要尽可能靠近 ITH 及 IC 信号地引脚。控制 IC 应该从供电电源地 (PGND) 有一个单独的信号地 (SGND)。开关节点 (例如 SW、BOOST、TG 和 BG) 应该远离敏感的小信号节点 (例如电流检测、反馈和 ITH 补偿走线)。

总结

对于开关模式电源而言，人们常常认为环路补偿设计是一项富有挑战性的任务。对于具快速瞬态要求的应用而言，设计具大带宽和充足稳定性裕度的电源是非常重要的。这通常是一个非常耗时的过程。本文讲述了一些关键概念，以帮助系统工程师了解这项任务，使用 LTpowerCAD 设计工具可将电源环路设计和优化变得简单得多。