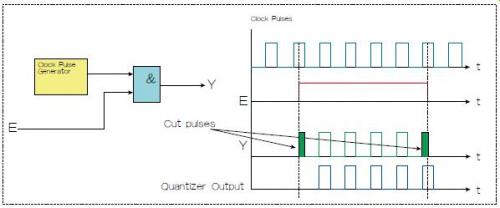
图1：两种选通脉冲串的方法，一种是使用选通信号E和与门（Y输出），一种是量化器（蓝色）。

本设计实例展示了一种用于综合异步选通电路的数学方法，这种电路可以在不改变脉冲宽度的条件下，从时钟信号中选通一个精确的脉冲串。这种电路被称为量化器。

根据量化器的工作原理做一个状态转换表（图2）。
 

图2：异步有限状态机（FSM）转换主表，其中1，2，3，4，5，6，7带圈的数字是稳定FSM状态号（G是时钟输入）。

图3：根据Mealy（左）和Moore（右）状态机做出的最终表格对。

借助图2并根据Mealy和Moore状态机可以做出最终的表格对（图3）。图中：

MC1：2-5-6-7和MC2：1-3-4是最大兼容集（根据Mealy状态机）；

MC1：5-7、MC2：1-2-6和MC3：1-3-4是最大兼容集（根据Moore状态机）。

从图3可以看到，Moore状态机的总覆盖率要求更大数量的最大兼容子集，也就是更糟糕。另一方面，第一个状态可以是MC2集和MC3集的一个部分，它代表了用于额外电路优化的机会。但无需进一步考虑这个问题。

现在就很容易画出压缩的状态转换表，并为Z编码的内存单元和输出选通信号Y画出卡诺-维奇图（图4）。
 

图4：卡诺-维奇图

根据卡诺-维奇图，为综合出来的电路写下逻辑公式：

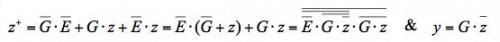
从这个公式可以看出，其中针对z+的最小项[E●z]不是多余的。它在最小项[G●E]和[G●z]之间扮演着反竞争桥的重要角色，可以消除G的所有边沿处的连续竞争。

式中：E=异步选通信号的反向输入；

G＝时钟；

Y＝量化器输出。

还可以增加一些额外的功能，比如FLAG.当FLAG是低电平时，脉冲串中的第一个脉冲不会被剪切掉，而是合并进脉冲串并且不会影响其宽度。当FLAG是高电平时，第一个脉冲被切掉，并排除在脉冲串以外。FLAG状态应保持不变直到下一个选通脉冲，因此设备有足够的时间来读取它，并用于进一步处理。