本文主要讨论测量50Hz交流暂态中功率因数的方法。电路应该是R-L类型。通过只获取电流波形，控制相对于电压波形的插入角在±10°公差范围内，就可能实现对功率因数的精确测量，并且不确定度很低。利用简单的数学表达式再加上电流峰值和均方根(RMS)值之间的关系即可计算出功率因数。

一些简单的操作指令

这种方法专门用于短路实验室，或需要在短路电流期间(如10个周期)计算功率因数之时。要注意的事项很少，比如在电流是对称的时候以及控制没有电流波形包络的时候测量RMS值。举例来说，发生器附近的短路次暂态;正弦波形状的电流等等。

让我们开始做测量：

通过在电压过零期间插入电路记录电流，记录时间为130ms;

得到电流峰值的绝对值;

得到电流的RMS值，比如90ms之后的值;测量一个完整周期内(20ms) 的RMS值;

计算峰值和RMS值的比值;

我们把这个比值称为Ikcr，将它插入下面这个公式：

再把这个称为cosφ的结果插入另外一个公式：

计算cosφ1和err φ之间的差值，结果就是功率因数值：

测量不确定度取决于与电流测量有关的不确定度。例如对于一个电流测量不确定度u为1.2%的系统来说， k=2功率因数时的扩展不确定度等于：

测量值从0.9到0.5时为±0.022

测量值从0.5到0.2时为±0.009

理论

这是RL电路的微分方程。如果v是具有下列方程的交流电压源：

那么方程[1]的解为：

其中：

φ是由arctg(Xl/R)确定的电路特征角：

γ是相对于电压波形的插入角;

τ是由L/R确定的电路的时间常数;

t是时间(自变量)，可以从0变到+∞。

通过分析方程[2]发现有两个分量，第一个是周期性的，对称的，第二个是单向分量，具有依赖于L/R比和插入角γ的渐减指数行为。当γ=0时，这个单向分量具有最大值。

让我们介绍一种只测量电流的RMS值和峰值就能计算角度φ的方法。这种方法无需任何其它测量，只需以± 10°的精度简单地控制插入角γ即可。

通过在0.9和0.1之间、并以0.05的步距改变角度φ的余弦值，并保持γ参数固定为0，就能利用微积分程序评估方程[2]的18个数字解。I可以是任何值。应该在时间t=0到t=0.13之间以步距为05E-5对每个解进行评估。对于得到的每个解，计算最大值和RMS值，如下图所示。

cos (φ=0,2)时的解。

cos (φ=0,5)时的解。

接着计算Imax/Irms的比值，我们称之为Ikcr(振幅因数);这个比值的变化范围从√2到2√2。

现在将计算出来的Ikcr值放到表格中，并与对应的cosφ值进行匹配

表1：cosφ和振幅因数Ikcr之间的关系。

微分方程[2]的数字解。

通过使用多项式近似技术，并搜索n次多项式，它将返回给定范围内任何Ikcr值的余弦值：

这个多项式应尽量减小方程[2]的实际数字解与计算值之间的误差。借助MATLAB或EXCEL之类的程序，就可以计算出不同次的各种多项式的系数，然后选择最好的一个。

图：重叠的多项式曲线。

经过分析发现，最佳的多项式近似是由5次曲线确定的，用MATLAB程序进行计算(最小平方方法)，它有以下表达式：

与5次曲线重叠的微分方程的数字解

不管怎样，有一个残留误差无法忽略：

多项式误差

为了解决这个问题，让我们搜索另外一个多项式，但现在它应适合残留误差点。

同样在经过分析之后发现，最好的多项式曲线具有下列表达式：

接下来通过计算[3]和[4]两个多项式之差就可以得到最终结果：

现在我们可以证明，这一最终结果的最大误差在方程[2]的数字解±0.065(uerr)之内。

残留误差。

仔细观察‘残留误差’和‘多项式误差’图形可以发现龙格现象。曲线在间隔边缘会增加误差。

测量的不确定度

现在看看不确定度的计算：唯一测量的参数是电流值(峰值和RMS)。它用相同的不确定度进行表征(测量系统是相同的)，它们之间的相关性是+1。因此通过应用公式：

那么：

借助这个值就可以计算由这两个多项式传播的不确定度：

其中cn是多项式的系数，它是与可忽略的不确定度一起考虑的。

现在再考虑由插入角误差γ给出的不确定度贡献。在测量0.5的功率因数时，相对于零的任何±10°变化都包含最大±0.0002 (2e-04) (uang)的cosφ值变化。

另外考虑由计算得到的多项式残留误差±0.065 (uerr)给出的另外一个贡献因素。

uang和uerr被认为都是均匀分布的。

现在我们已经有充足条件做最终计算了：

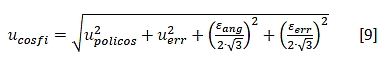
我们可以分析不确定度趋势和每种贡献因素的加权。

不确定度的变化。

不确定度的贡献因素。

计算结果

鉴于不确定度趋势在cosφ变化点的行为，决定将不确定度分为两个间隔;举例来说，将1.2%的不确定度u用于电流读取，k=2时与cos测量相关的扩展不确定度是：

cos φ从0.9到0.5时为±0.022

cos φ从0.5到0.2时为±0.009

本文小结

使用不确定度约为2%-3%的电流测量链可以实现精确的功率因数测量。获取这些不确定度值不是太困难或太费劲。

也可以用机械装置插入公差为±10°的电路，比如用直流电流提升的电流接触器;静态开关不是强制要求的。

多项式可以用任何简单的微积分程序进行计算，如EXCEL，或用带数字函数的示波器。

从0.9到0.2的测量范围覆盖了大部分低压标准要求。

这种测量通过电压测量实现，因此是完全独立的。

使用示波器计算相位差不是简单的一次操作，它暗含了精确的电压测量和光标的使用。