输入功率和RMS电流测量低成本解决方案_深圳市永阜康科技有限公司

今天，包括离线电源真实输入功率和输入RMS电流测量在内的能耗实时测量，正变得愈加重要。这些测量可用于调节供电和优化能源利用。例如，安装有许多服务器的一些数据中心对服务器层辅助功耗测量就很感兴趣，因为这样可以实现低成本数据服务，并对低功耗工作期间的处理能力进行智能的管理。输入功率和电流的一般测量方法是使用一个专用功率计芯片和附加检测电路。尽管功率计芯片能够提供可接受的测量结果，但它大大增加了成本和设计工作量。本文为您介绍一种新颖、低成本且精确的输入功率和RMS电流测量解决方案。它使用现有的数字功率因数校正（PFC）控制芯片和硬件，以及简单的两点校准和优化数学计算。这样便可提供优异的测量精确度，并极大降低成本和减少工作量，同时不影响正常的PFC控制。

测量装置
图1显示了由一个数字控制器进行电源隔离控制的传统PFC装置。输入线路和中性点电压通过一个衰减网络检测，之后由两个单独的模数转换器 (ADC) 输入采样。电流信号经由一个分流器检测，然后被信号调节电路放大和滤波。之后，连接至一个ADC进行电流环路控制。由于输入电压和电流测量已经具备，因此可用它们来测量输入功率和RMS电流。一样的传统PFC装置用于这些测量，无需传统专用功率计芯片和附加检测电路。

图1 输入功率和电流测量PFC装置

电流测量与校准
电流检测信号调节电路（图1）一般由一个运算放大器和一个低通滤波器组成，目的是放大小检测信号和去除高频噪声。之后，通过一个ADC测量该信号，并以ADC计数报告。为了获得真实的电流值，需把ADC计数转换为以安培为单位的电流。ADC计数与安培的关系可由原理图推导得出；但是，组件容差可能会使测量精确度变得不可接受。因此，需要进行一次校准。

电路如图1所示，在任何时候，分流器的输入电流（单位毫安培）均为：

其中，ki为电流检测增益或者斜率，Ci为ADC转换输出（计数），而mi为电流检测偏移量。

直流（DC）输入恒定时，平均值等于瞬时值，因此方程式1仍然有效：

方程式2表明，DC电源可用于对电流测量电路进行校准。恒定DC电源用于PFC输入，先使用25%负载然后再75%负载进行测量。为了方便比较，使用一个电表对两种负载状态的实际输入电流进行基准测量。另外，读取对两种负载状态的ADC转换计数输出，以确定数字控制器的精确度。控制器使用下列数学关系。25%负载状态时：

75%负载状态时：

使用方程式3和4计算电流斜率和偏移量：

计算得到的ki和mi为小数，小于1，而PFC应用的大多数数字控制器均使用定点数学计算。为了降低计算的化整误差和保持足够高的精确度，把这些小数值乘以2N，然后四舍五入为最为接近的整数。例如，如果PFC电路的电流检测增益和偏移量计算得到为ki= 1.59和mi= 229.04，则ki乘以28，然后四舍五入为407；mi乘以20。电流斜率和偏移量分别为：

和

其中，iin_slope = 407，iin_slope_shift = 8，iin_offset = 229，而iin_offset_shift = 0。
计算得到输入功率和RMS电流以后，如果ki和mi为倍数，则不要直接使用它们，你可以先使用iin_slope和iin_offset来做乘法运算。然后，使用iin_slope_shift和iin_offset_shift来转换结果。例如，不要使用y = ki× x + mi× z进行计算，而要使用下面的计算方法：

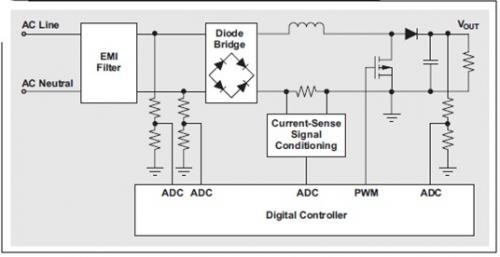
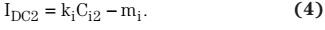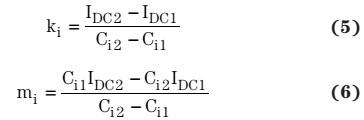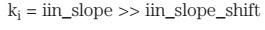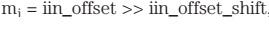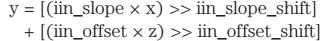输入电压测量与校准
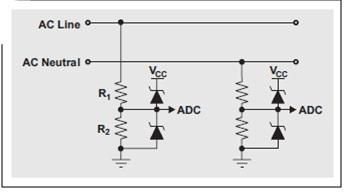
电压检测电路十分简单，它可以只是一个分压器，如图2所示。一般，会有一些箝制二极管来保护ADC引脚。由于二极管的反向漏电流影响ADC的测量精确度，因此应选择使用低反向漏电流的二极管。

图2 AC输入电压检测电路

任何时候，输入电压均为：

其中，kv为电压检测增益，Cv为ADC转换输出（计数），而mv则为电压检测偏移量。Kv和mv的校准方法类似，都是对电流检测增益和偏移量进行校准。但是，一种更加简单的方法是只需根据原理图进行计算。由于没有了校准，因此分压器使用的电阻会影响测量精确度。我们推荐把低容差电阻器用作分压器，例如：0.1%容差。

一个12位ADC和2.5V基准电压的数字控制器，输入电压被分压器衰减至2.5V以下。这样，经过衰减的信号被ADC转换为数字信号。因此：

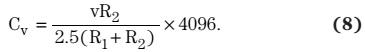
重写方程式8之后，输入电压为：

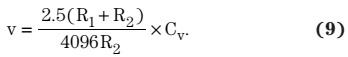
因此：

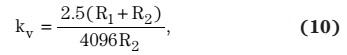
以及：

与输入电流测量类似，需要对电压检测增益和偏移量进行一些操作，以使其适应定点微处理器，并降低计算误差。

VIN和IIN相互关系
真实输入功率定义为：

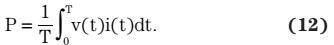
使用离散格式后，其定义为：

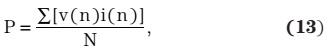
其中，N为总采样数。方程式13表明，需同时对VIN和IIN采样。但是，VIN和IIN却是由两个不同的ADC通道在不同时间采样。即使是很小的时间差，也会引起测量误差。在一些数字控制器中，例如：TI UCD3138等，具有一种被称作“双采样保持”的机制，其允许两种通道同时采样，从而消除了这种误差。

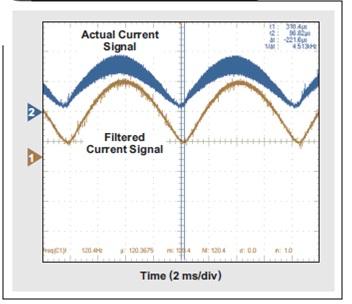
由于电流检测电路中使用了低通滤波器，受测电流信号出现延迟，并且实际电流存在相移。图3显示了这种情况，图中，通道2为实际电流信号，通道1为经过放大的相同信号，其随后经低通滤波器输出。该放大信号有约220 μs的相位延迟。需要对这种延迟进行补偿，否则它会影响输入功率测量的精确度。一种简单的补偿方法是，让VIN-sense信号延迟约220μs，然后使用该经过延迟的VIN信号来进行输入功率计算。所以，如果每隔20μs测量一次VIN，则需要对其延迟220/20 =11次。

图3 电流检测相移

真实输入功率计算
组合方程式1、7和13，得到：

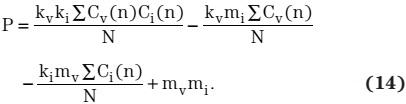
VIN和IIN由ADC在标准中断环路中测量，其具有一定的限制时间，并且主要用于PFC环路控制。因此，为了节省CPU计算时间和防止标准中断环路溢出，仅在该环路中计算Cv(n)C
i(n)。另外，方程式14的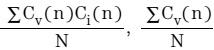以及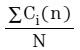各项，使用无限脉冲响应（IIR）滤波器来实现。在背景环路中完成真实输入功率的最终计算。

输入RMS电流计算
图1所示数字控制器所进行的电流测量并不代表总输入电流，因为电磁干扰（EMI）滤波器中电容的作用未包括在内。在高线压和轻负载条件下，这种滤波器电流不再可以忽略不计，必须将其包括进来，以实现精确的输入电流报告。

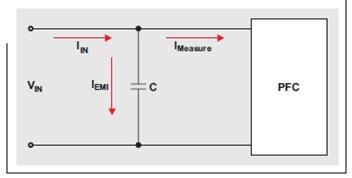
图4显示了一种简化版的EMI滤波器，我们去除了电感器，并使用一个单电容器（C）来代替总电容。图中，IEMI为EMI电容器的RMS电抗性电流，IMeasure为数字控制器测量的输入RMS电流，而IIN则为总输入RMS电流。

图4 简化版EMI滤波器的电流

EMI滤波器产生的电抗性电流为：

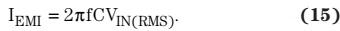
为了计算EMI电容器的电抗性电流，首先需要知道输入电压频率。AC线压和中性点电压由两个ADC通道检测，然后通过固件整流。通过对比两个ADC结果，我们可以发现零交叉。由于使用固定率对输入电压进行采样，因此可以通过计数两个连续零交叉点之间的采样数来计算AC频率。一旦知道输入电压频率，便可计算EMI电容器的电抗性电流：

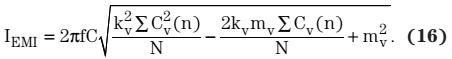
如前所述，在标准中断环路中测量电压，因此为了节省CPU计算时间和防止该环路溢出，仅在其内计算。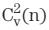
方程式16的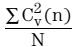和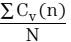项，通过IIR滤波器实现。在背景环路中计算最终EMI电抗性电流。ADC测得电流为：

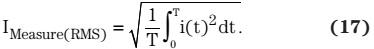
使用离散格式，它可以写为：

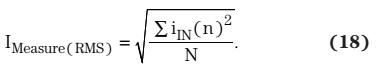
组合方程式1和18得到：

所前所述，在标准中断环路中测量电流，因此仅在该环路中计算。
方程式19的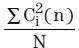和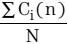项通过IIR滤波器实现。

最后，把EMI滤波器的电抗性电流（IEMI）加上IMeasure（RMS），得到总输入电流。IEMI领先受测电流（IMeasure（RMS））90º，因此，在背景环路中计算最终输入RMS电流。

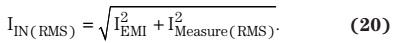
测试结果
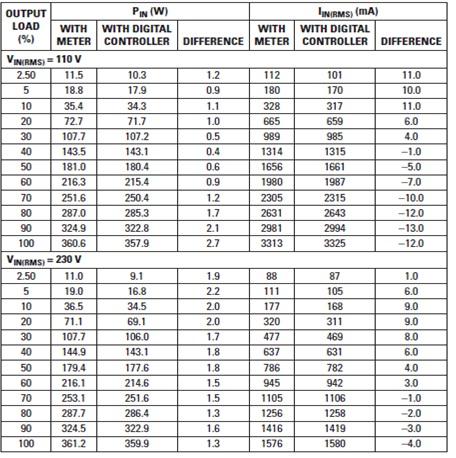
这种输入功率和RMS电流测量方法在一个360W的PFC评估模块上进行了测试。结果（表1）表明，这种方法拥有优异的测量精确度。

表1 输入功率和RMS电流测量的测试结果

结论
我们为您介绍了一种低成本但却精确的离线电源输入功率和RMS电流测量方法。这种方法使用现有PFC控制器芯片和硬件，无需传统的专用功率计芯片和额外的检测电路，并且不影响正常的PFC控制。另外，它还具有如下一些特点：

    极低的成本
    简单的两点校准
    使用双采样保持，VIN和IIN同时采样
    固件EMI电流补偿
    固件电流检测，相移补偿
    优化的数学计算，CPU使用开销较少